K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
18 tháng 6 2016
pt <=> x(1+2+3+4+5..+900)=3649050
<=> x.(1+900).900/2=3649050<=> x.405450=3649050
=> x=9
18 tháng 6 2016
x+2x+3x+4x+...+900x=3649050
=> x(1 + 2 + 3 + ... + 900) = 3649050
=> x.(900 + 1)(900 - 1 + 1)/2 = 3649050
=> x.405450 = 3649050
=> x = 9
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 5 2019
ĐKXĐ: \(\left[{}\begin{matrix}x\ge7\\x\le-2\end{matrix}\right.\)
- Nếu \(2x-1< 0\Leftrightarrow x< \frac{1}{2}\) thì \(\left\{{}\begin{matrix}VT\ge0\\VP< 0\end{matrix}\right.\) BPT hiển nhiên đúng
Kết hợp điều kiện đề bài ta được \(x\le-2\)
- Nếu \(2x-1\ge0\Rightarrow x\ge\frac{1}{2}\) hai vế BPT đều ko âm, bình phương 2 vế:
\(\Leftrightarrow x^2-5x-14\ge4x^2-4x+1\)
\(\Leftrightarrow3x^2+x+15\le0\) (vô nghiệm)
Vậy nghiệm của BPT đã cho là \(x\le-2\)
22 tháng 12 2022
=>2x-2y=1 và 2x+2y=-1
=>4x=0 và x-y=1/2
=>x=0 và y=0-1/2=-1/2
22 tháng 12 2022
Có cách bấm máy tính 570vn plus không ạ em cần biết cách bấm máy tính ạ
28 tháng 8 2020
a,gọi I là trung điểm của AB, vì A và B là 2 điểm cố định => I cũng cố định
=> vt IA+vt IB=0
=>|vt MA+vtMB|=|vtMA-vtMB|
<=> |vtMI+vtIA+vtMI+vtIB|=|vtMI+vtMA-vtMI-vtIB|
<=>|2.vtMI|=|vtBA|
<=> 2,MI=BA
=> MI=BA/2
=> M thuộc (I;AB/2)
NA
4
I
1 tháng 4 2020
mình nghĩ đề nó như thế này
\(\sqrt{a^2+b^2}-\sqrt{c^2+d^2}\ge\sqrt{\left(a+c\right)^2-\left(b+d^{ }\right)^2}\)
hai zế BĐT ko âm nên bình phương 2 zế ta có
\(a^2+b^2+c^2+d^2+2\sqrt{\left(a^2+b^2\right)\left(c^2+d^2\right)}\ge a^2+2ac+c^2+b^2+2bd+d^2\)
\(\Leftrightarrow\sqrt{\left(a^2+b^2\right)\left(c^2+d^2\right)}\ge ac+bd\left(1\right)\)
Nếu \(ac+bd< 0\)thì BĐT đc c/m
Nêu \(ac+bd\ge0\left(1\right)\Leftrightarrow\left(a^2+b^2\right)\left(c^2+d^2\right)\ge a^2c^2+b^2d^2+2acbd\)
\(\Leftrightarrow a^2c^2+a^2d^2+b^2c^2+b^2d^2\ge a^2c^2+b^2d^2+2acbd\)
\(\Leftrightarrow a^2d^2+b^2c^2-2acbd\ge0\Leftrightarrow\left(ad-bc\right)^2\ge0\)( luôn đúng )
dấu = xảy ra khi \(ad=bc\Leftrightarrow\frac{a}{b}=\frac{c}{d}\)
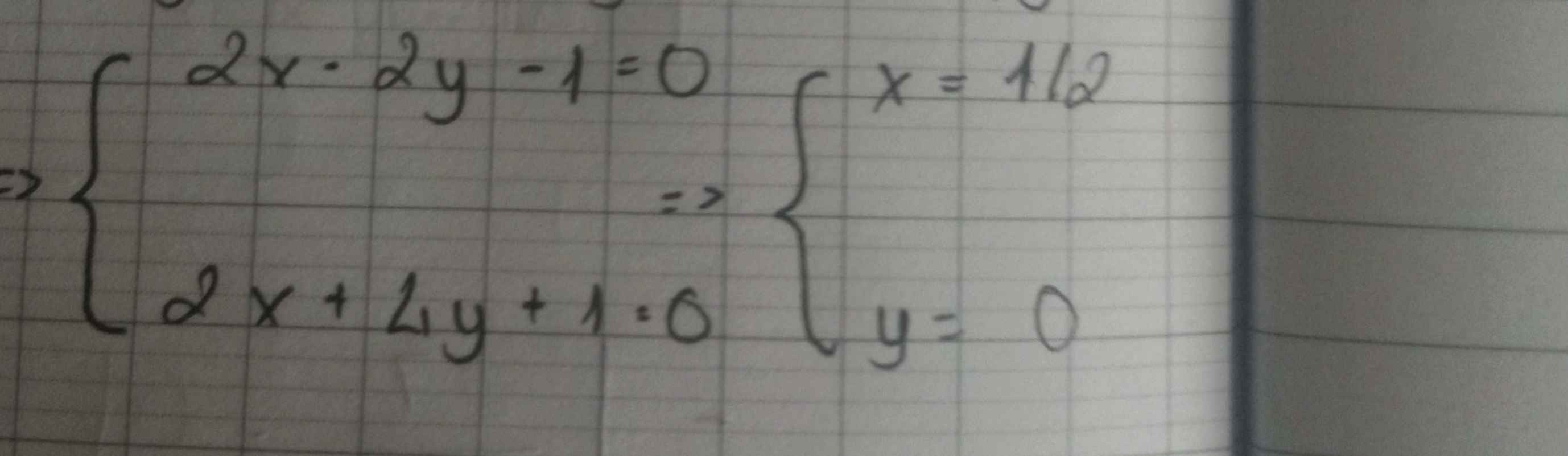
\(A=\left\{-1;0;1\right\}\\ \left(5x-3x^2\right)\left(x^2-2x-3\right)=0\\ \Leftrightarrow x\left(5-3x\right)\left(x-3\right)\left(x+1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{5}{3}\left(ktm\right)\\x=3\\x=-1\end{matrix}\right.\\ \Leftrightarrow B=\left\{-1;0;3\right\}\)
Do đó \(A\cap B=\left\{-1;0\right\};A\cup B=\left\{-1;0;1;3\right\};A\B=\left\{1\right\};B\A=\left\{3\right\}\)