Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Sắp xếp lại dãy số liệu theo thứ tự không giảm:

Tứ phân vị thứ nhất là: \(\frac{1}{2}\left( {{x_5} + {x_6}} \right) = \frac{1}{2}\left( {11 + 11} \right) = 11\)
Tứ phân vị thứ hai là: \(\frac{1}{2}\left( {{x_{10}} + {x_{11}}} \right) = \frac{1}{2}\left( {14 + 14} \right) = 14\)
Tứ phân vị thứ ba là: \(\frac{1}{2}\left( {{x_{15}} + {x_{16}}} \right) = \frac{1}{2}\left( {21 + 22} \right) = 21,5\)
b)

c) Do số trận đấu là số nguyên nên ta hiệu chỉnh như sau:

Tổng trận đấu là: \(n = 4 + 8 + 2 + 6 = 20\).
Gọi \({x_1};{x_2};...;{x_{20}}\) là điểm số của các trận đấu được xếp theo thứ tự không giảm.
Ta có:
\({x_1},...,{x_4} \in \begin{array}{*{20}{c}}{\left[ {5,5;10,5} \right)}\end{array};{x_5},...,{x_{12}} \in \begin{array}{*{20}{c}}{\left[ {10,5;15,5} \right)}\end{array};{x_{13}},{x_{14}} \in \begin{array}{*{20}{c}}{\left[ {15,5;20,5} \right)}\end{array};{x_{15}},...,{x_{20}} \in \begin{array}{*{20}{c}}{\left[ {20,5;25,5} \right)}\end{array}\)
• Tứ phân vị thứ hai của dãy số liệu là: \(\frac{1}{2}\left( {{x_{10}} + {x_{11}}} \right)\)
Ta có: \(n = 20;{n_m} = 8;C = 4;{u_m} = 10,5;{u_{m + 1}} = 15,5\)
Do \({x_{10}},{x_{11}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {10,5;15,5} \right)}\end{array}}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 10,5 + \frac{{\frac{{20}}{2} - 4}}{8}.\left( {15,5 - 10,5} \right) = 14,25\)
• Tứ phân vị thứ nhất của dãy số liệu là: \(\frac{1}{2}\left( {{x_5} + {x_6}} \right)\).
Ta có: \(n = 20;{n_m} = 8;C = 4;{u_m} = 10,5;{u_{m + 1}} = 15,5\)
Do \({x_5},{x_6} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {10,5;15,5} \right)}\end{array}}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 10,5 + \frac{{\frac{{20}}{4} - 4}}{8}.\left( {15,5 - 10,5} \right) = 11,125\)
• Tứ phân vị thứ ba của dãy số liệu là: \(\frac{1}{2}\left( {{x_{15}} + {x_{16}}} \right)\).
Ta có: \(n = 20;{n_j} = 6;C = 4 + 8 + 2 = 14;{u_j} = 20,5;{u_{j + 1}} = 25,5\)
Do \({x_{15}},{x_{16}} \in \begin{array}{*{20}{c}}{\left[ {20,5;25,5} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 20,5 + \frac{{\frac{{3.20}}{4} - 14}}{6}.\left( {25,5 - 20,5} \right) \approx 21,3\)

a) Sắp xếp lại dãy số liệu theo thứ tự không giảm:

Tứ phân vị thứ nhất là: \(\frac{1}{2}\left( {{x_6} + {x_7}} \right) = \frac{1}{2}\left( {8,9 + 9,2} \right) = 9,05\)
Tứ phân vị thứ hai là: \(\frac{1}{2}\left( {{x_{13}} + {x_{14}}} \right) = \frac{1}{2}\left( {10,7 + 10,9} \right) = 10,8\)
Tứ phân vị thứ ba là: \(\frac{1}{2}\left( {{x_{18}} + {x_{19}}} \right) = \frac{1}{2}\left( {12,2 + 12,5} \right) = 12,35\)
b)

c) Tổng số nhân viên văn phòng là: \(n = 3 + 6 + 8 + 7 = 24\).
Gọi \({x_1};{x_2};...;{x_{24}}\) là lương tháng của các nhân viên văn phòng được xếp theo thứ tự không giảm.
Ta có:
\({x_1},{x_2},{x_3} \in \begin{array}{*{20}{l}}{\left[ {6;8} \right)}\end{array};{x_4},...,{x_9} \in \begin{array}{*{20}{l}}{\left[ {8;10} \right)}\end{array};{x_{10}},...,{x_{17}} \in \begin{array}{*{20}{l}}{\left[ {10;12} \right)}\end{array};{x_{18}},...,{x_{24}} \in \begin{array}{*{20}{l}}{\left[ {12;14} \right)}\end{array}\)
• Tứ phân vị thứ hai của dãy số liệu là: \(\frac{1}{2}\left( {{x_{13}} + {x_{14}}} \right)\)
Ta có: \(n = 24;{n_m} = 8;C = 3 + 6 = 9;{u_m} = 10;{u_{m + 1}} = 12\)
Do \({x_{13}},{x_{14}} \in \begin{array}{*{20}{l}}{\left[ {10;12} \right)}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 10 + \frac{{\frac{{24}}{2} - 9}}{8}.\left( {12 - 10} \right) = 10,75\)
• Tứ phân vị thứ nhất của dãy số liệu là: \(\frac{1}{2}\left( {{x_6} + {x_7}} \right)\).
Ta có: \(n = 24;{n_m} = 6;C = 3;{u_m} = 8;{u_{m + 1}} = 10\)
Do \({x_6},{x_7} \in \begin{array}{*{20}{l}}{\left[ {8;10} \right)}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 8 + \frac{{\frac{{24}}{4} - 3}}{6}.\left( {10 - 8} \right) = 9\)
• Tứ phân vị thứ ba của dãy số liệu là: \(\frac{1}{2}\left( {{x_{18}} + {x_{19}}} \right)\).
Ta có: \(n = 24;{n_j} = 7;C = 3 + 6 + 8 = 17;{u_j} = 12;{u_{j + 1}} = 14\)
Do \({x_{18}},{x_{19}} \in \begin{array}{*{20}{l}}{\left[ {12;14} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 12 + \frac{{\frac{{3.24}}{4} - 17}}{7}.\left( {14 - 12} \right) \approx 12,3\)

Tổng số học sinh: \(n = 8 + 10 + 16 + 24 + 13 + 7 + 4 = 82\)
• Điểm trung bình môn Toán của các học sinh lớp 11 trên là:
\(\bar x = \frac{{8.6,75 + 10.7,25 + 16.7,75 + 24.8,25 + 13.8,75 + 7.9,25 + 4.9,75}}{{82}} = 8,12\)
• Nhóm chứa mốt của mẫu số liệu trên là nhóm \(\left[ {8;8,5} \right)\).
Do đó: \({u_m} = 8;{n_{m - 1}} = 16;{n_m} = 24;{n_{m + 1}} = 13;{u_{m + 1}} - {u_m} = 8,5 - 8 = 0,5\)
Mốt của mẫu số liệu ghép nhóm là:
\({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right) = 8 + \frac{{24 - 16}}{{\left( {24 - 16} \right) + \left( {24 - 13} \right)}}.0,5 \approx 8,21\)
• Gọi \({x_1};{x_2};...;{x_{82}}\) là điểm của các học sinh lớp 11 được xếp theo thứ tự không giảm.
Ta có:
\(\begin{array}{l}{x_1},...,{x_8} \in \begin{array}{*{20}{c}}{\left[ {6,5;7} \right)}\end{array};{x_9},...,{x_{18}} \in \begin{array}{*{20}{c}}{\left[ {7;7,5} \right)}\end{array};{x_{19}},...,{x_{34}} \in \begin{array}{*{20}{c}}{\left[ {7,5;8} \right)}\end{array};{x_{35}},...,{x_{58}} \in \begin{array}{*{20}{c}}{\left[ {8;8,5} \right)}\end{array};\\{x_{59}},...,{x_{71}} \in \begin{array}{*{20}{c}}{\left[ {8,5;9} \right)}\end{array};{x_{72}},...,{x_{78}} \in \begin{array}{*{20}{c}}{\left[ {9;9,5} \right)}\end{array};{x_{79}},...,{x_{82}} \in \begin{array}{*{20}{c}}{\left[ {9,5;10} \right)}\end{array}\end{array}\)
Tứ phân vị thứ hai của dãy số liệu là: \(\frac{1}{2}\left( {{x_{41}} + {x_{42}}} \right)\)
Ta có: \(n = 82;{n_m} = 24;C = 8 + 10 + 16 = 34;{u_m} = 8;{u_{m + 1}} = 8,5\)
Do \({x_{41}},{x_{42}} \in \begin{array}{*{20}{l}}{\left[ {8;8,5} \right)}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 8 + \frac{{\frac{{82}}{2} - 34}}{{24}}.\left( {8,5 - 8} \right) \approx 8,15\)
Tứ phân vị thứ nhất của dãy số liệu là: \({x_{21}}\).
Ta có: \(n = 82;{n_m} = 16;C = 8 + 10 = 18;{u_m} = 7,5;{u_{m + 1}} = 8\)
Do \({x_{21}} \in \begin{array}{*{20}{l}}{\left[ {7,5;8} \right)}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 7,5 + \frac{{\frac{{82}}{4} - 18}}{{16}}.\left( {8 - 7,5} \right) \approx 7,58\)
Tứ phân vị thứ ba của dãy số liệu là: \({x_{62}}\).
Ta có: \(n = 82;{n_j} = 13;C = 8 + 10 + 16 + 24 = 58;{u_j} = 8,5;{u_{j + 1}} = 9\)
Do \({x_{62}} \in \begin{array}{*{20}{l}}{\left[ {8,5;9} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 8,5 + \frac{{\frac{{3.82}}{4} - 58}}{{13}}.\left( {9 - 8,5} \right) \approx 8,63\)

Cỡ mẫu là: \(n = 21\).
Suy ra tứ phân vị thứ nhất \({Q_1}\)là \(\frac{{{x_5} + {x_6}}}{2}\). Do \({x_5};{x_6}\) đều thuộc nhóm [5;10) nên từ phân vị thứ nhất thuộc nhóm [5;10).
Tứ phân vị thứ ba \({Q_3}\) là \(\frac{{{x_{16}} + {x_{17}}}}{2}\) . Do \({x_{16}};\;{x_{17}}\)đều thuộc nhóm [10; 15) nên tứ phân vị thứ ba thuộc nhóm [10; 15).

Tham khảo:
a) Sắp xếp lại dãy số liệu theo thứ tự không giảm:
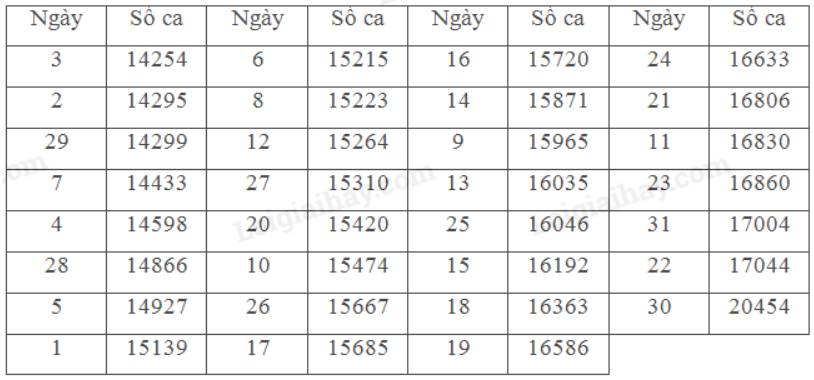
Số trung bình của số liệu là: \(\bar x \approx 15821,87\)
Tứ phân vị thứ nhất là: \({x_8} = 15139\)
Tứ phân vị thứ hai là: \({x_{16}} = 15685\)
Tứ phân vị thứ ba là: \({x_{24}} = 16586\)
Mẫu số liệu có 1 giá trị ngoại lệ.
b)

c) Ta có:

• Số ca nhiễm mới SARS-CoV-2 trung bình trong tháng 12/2021 tại Việt Nam là:
\(\bar x = \frac{{14.14,74 + 14.16,25 + 2.17,75 + 0.19,25 + 1.20,75}}{{31}} \approx 15,81\)
• Gọi \({x_1};{x_2};...;{x_{31}}\) số ca nhiễm mới SARS-CoV-2 mỗi ngày trong tháng 12/2021 tại Việt Nam được xếp theo thứ tự không giảm.
Ta có: \({x_1},...,{x_{14}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{l}}{\begin{array}{*{20}{c}}{\left[ {14;15,5} \right)}\end{array}}\end{array}}\end{array};{x_{15}},...,{x_{28}} \in \begin{array}{*{20}{l}}{\begin{array}{*{20}{c}}{\left[ {15,5;17} \right)}\end{array}}\end{array};{x_{29}},{x_{30}} \in \begin{array}{*{20}{c}}{\left[ {17;18,5} \right)}\end{array};{x_{31}} \in \begin{array}{*{20}{l}}{\begin{array}{*{20}{c}}{\left[ {20;21,5} \right)}\end{array}}\end{array}\)
Tứ phân vị thứ hai của dãy số liệu là: \({x_{16}}\)
Ta có: \(n = 31;{n_m} = 14;C = 14;{u_m} = 15,5;{u_{m + 1}} = 17\)
Do \({x_{16}} \in \begin{array}{*{20}{c}}{\left[ {15,5;17} \right)}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 15,5 + \frac{{\frac{{31}}{2} - 14}}{{14}}.\left( {17 - 15,5} \right) \approx 15,66\)
Tứ phân vị thứ nhất của dãy số liệu là: \({x_8}\).
Ta có: \(n = 31;{n_m} = 14;C = 0;{u_m} = 14;{u_{m + 1}} = 15,5\)
Do \({x_8} \in \begin{array}{*{20}{c}}{\left[ {14;15,5} \right)}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 14 + \frac{{\frac{{31}}{4} - 0}}{{14}}.\left( {15,5 - 14} \right) \approx 14,83\)
Tứ phân vị thứ ba của dãy số liệu là: \({x_{24}}\).
Ta có: \(n = 31;{n_j} = 14;C = 14;{u_j} = 15,5;{u_{j + 1}} = 17\)
Do \({x_{24}} \in \begin{array}{*{20}{c}}{\left[ {15,5;17} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 15,5 + \frac{{\frac{{3.31}}{4} - 14}}{{14}}.\left( {17 - 15,5} \right) \approx 16,49\)

Ta có:
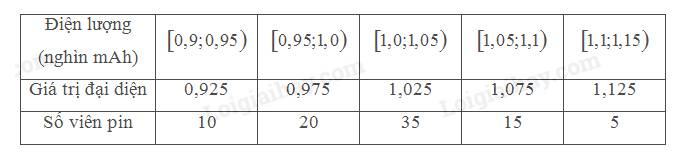
Tổng số viên pin là: \(n = 10 + 20 + 35 + 15 + 5 = 85\).
• Điện lượng trung bình của một số viên pin tiểu sau khi ghép nhóm là:
\(\bar x = \frac{{10.0,925 + 20.0,975 + 35.1,025 + 15.1,075 + 5.1,125}}{{85}} \approx 1,02\left( {mAh} \right)\)
• Nhóm chứa mốt của mẫu số liệu trên là nhóm \(\begin{array}{*{20}{c}}{\left[ {1,0;1,05} \right)}\end{array}\).
Do đó: \({u_m} = 1,0;{n_{m - 1}} = 20;{n_m} = 35;{n_{m + 1}} = 15;{u_{m + 1}} - {u_m} = 1,05 - 1,0 = 0,05\)
Mốt của mẫu số liệu ghép nhóm là:
\({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right) = 1,0 + \frac{{35 - 20}}{{\left( {35 - 20} \right) + \left( {35 - 15} \right)}}.0,05 \approx 1,02\left( {mAh} \right)\)
Gọi \({x_1};{x_2};...;{x_{85}}\) là điện lượng của các viên pin được xếp theo thứ tự không giảm.
Ta có:
\(\begin{array}{l}{x_1},...,{x_{10}} \in \begin{array}{*{20}{c}}{\left[ {0,9;0,95} \right)}\end{array};{x_{11}},...,{x_{30}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {0,95;1,0} \right)}\end{array}}\end{array};{x_{31}},...,{x_{65}} \in \begin{array}{*{20}{c}}{\left[ {1,0;1,05} \right)}\end{array};\\{x_{66}},...,{x_{80}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {1,05;1,1} \right)}\end{array}}\end{array};{x_{81}},...,{x_{85}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {1,1;1,15} \right)}\end{array}}\end{array}}\end{array}\end{array}\)
• Tứ phân vị thứ hai của dãy số liệu là: \({x_{43}}\)
Ta có: \(n = 85;{n_m} = 35;C = 10 + 20 = 30;{u_m} = 1,0;{u_{m + 1}} = 1,05\)
Do \({x_{43}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {1,0;1,05} \right)}\end{array}}\end{array}}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 1,0 + \frac{{\frac{{85}}{2} - 30}}{{35}}.\left( {1,05 - 1,0} \right) \approx 1,02\)
• Tứ phân vị thứ nhất của dãy số liệu là: \(\frac{1}{2}\left( {{x_{21}} + {x_{22}}} \right)\).
Ta có: \(n = 85;{n_m} = 20;C = 10;{u_m} = 0,95;{u_{m + 1}} = 1,0\)
Do \({x_{21}},{x_{22}} \in \begin{array}{*{20}{c}}{\left[ {0,95;1,0} \right)}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 0,95 + \frac{{\frac{{85}}{4} - 10}}{{20}}.\left( {1,0 - 0,95} \right) \approx 0,98\)
• Tứ phân vị thứ ba của dãy số liệu là: \(\frac{1}{2}\left( {{x_{64}} + {x_{65}}} \right)\).
Ta có: \(n = 85;{n_j} = 35;C = 10 + 20 = 30;{u_j} = 1,0;{u_{j + 1}} = 1,05\)
Do \({x_{64}},{x_{65}} \in \begin{array}{*{20}{c}}{\left[ {1,0;1,05} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 1,0 + \frac{{\frac{{3.85}}{4} - 30}}{{35}}.\left( {1,05 - 1,0} \right) \approx 1,048\)

Tham khảo:
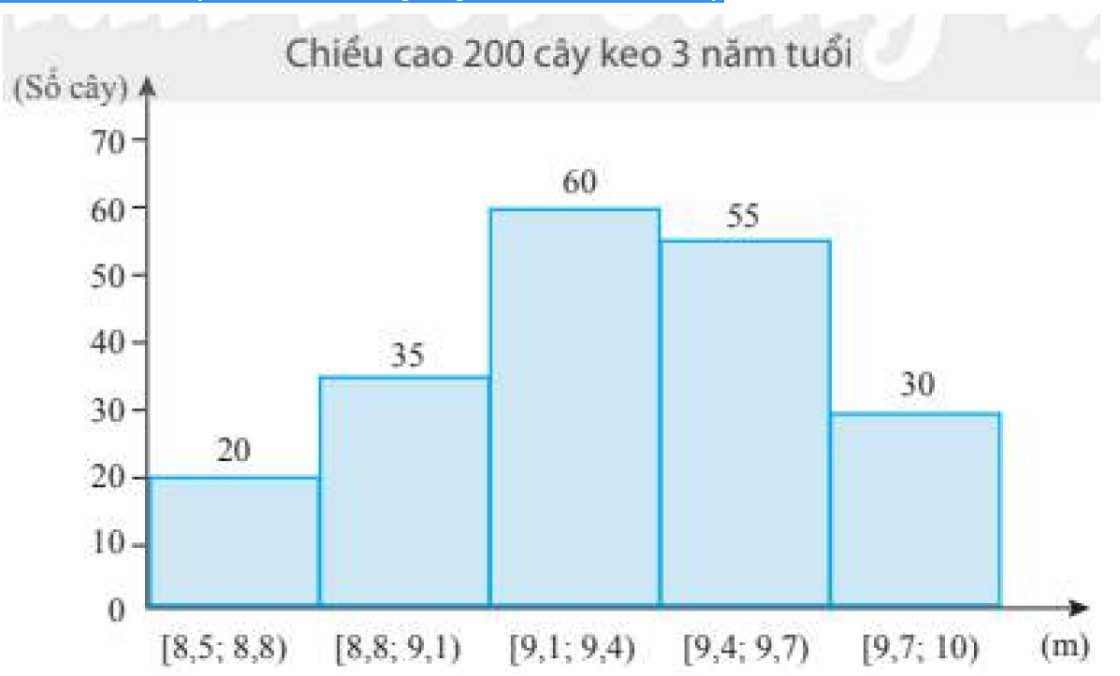
Chiều cao của 200 cây keo 3 năm tuổi được thống kê trong bảng sau:

Chiều cao của 200 cây keo 3 năm tuổi sau khi ghép nhóm là:
\(\bar x = \frac{{20.8,65 + 35.8,95 + 60.9,25 + 55.9,55 + 30.9,85}}{{200}} = 9,31\left( m \right)\)
Nhóm chứa mốt của mẫu số liệu trên là nhóm \(\begin{array}{*{20}{c}}{\left[ {9,1;9,4} \right)}\end{array}\).
Do đó: \({u_m} = 9,1;{n_{m - 1}} = 35;{n_m} = 60;{n_{m + 1}} = 55;{u_{m + 1}} - {u_m} = 9,4 - 9,1 = 0,3\)
Mốt của mẫu số liệu ghép nhóm là:
\({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right) = 9,1 + \frac{{60 - 35}}{{\left( {60 - 35} \right) + \left( {60 - 55} \right)}}.0,3 = 9,35\)
Vậy chiều cao của 200 cây keo 3 năm tuổi nhiều nhất là 9,35 mét.

Số cuộc gọi của người đó trong một tuần là \(n = 8 + 10 + 7 + 5 + 2 + 1 = 33\).
Gọi \({x_1};{x_2};...;{x_{33}}\) là thời gian thực hiện cuộc gọi của người đó trong một tuần được xếp theo thứ tự không giảm.
Ta có:
\({x_1},...,{x_8} \in \left[ {0;60} \right);{x_9},...,{x_{18}} \in \left[ {60;120} \right);{x_{19}},...,{x_{25}} \in \left[ {120;180} \right);{x_{26}},...,{x_{30}} \in \left[ {180;240} \right);\) \({x_{31}},{x_{32}} \in \left[ {240;300} \right);{x_{33}} \in \left[ {300;360} \right)\).
• Tứ phân vị thứ hai của dãy số liệu là: \({x_{17}}\) thuộc nhóm \(\begin{array}{*{20}{l}}{\left[ {60;120} \right)}\end{array}\)
Ta có: \(n = 33;{n_m} = 10;C = 8;{u_m} = 60;{u_{m + 1}} = 120\)
Tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 60 + \frac{{\frac{{33}}{2} - 8}}{{10}}.\left( {120 - 60} \right) = 111\)
• Tứ phân vị thứ nhất của dãy số liệu là: \(\frac{1}{2}\left( {{x_8} + {x_9}} \right)\).
Do \({x_8} \in \left[ {0;60} \right),{x_9} \in \left[ {60;120} \right)\) nên tứ phân vị thứ nhất của dãy số liệu là: \({Q_1} = 60\).
• Tứ phân vị thứ ba của dãy số liệu là: \(\frac{1}{2}\left( {{x_{25}} + {x_{26}}} \right)\).
Do \({x_{25}} \in \left[ {120;180} \right),{x_{26}} \in \left[ {180;240} \right)\) nên tứ phân vị thứ ba của dãy số liệu là: \({Q_3} = 180\).

Tham khảo:
Khoảng biến thiên của mẫu số liệu trên là \(R = 29 - 10 = 19\).
Độ dài mỗi nhóm \(L > \frac{R}{k} = \frac{{19}}{5} = 3,8\).
Ta chọn \(L = 4\) và chia dữ liệu thành các nhóm: \(\left[ {10;14} \right),\left[ {14;18} \right),\left[ {18;22} \right),\left[ {22;26} \right),\left[ {26;30} \right)\).
Khi đó ta có bảng tần số ghép nhóm sau:












a, Bảng tần số ghép nhóm cho mẫu số liệu trên có tám nhóm ứng với tám nửa khoảng:
b, - Trung bình cộng là:
\(\overline{x}=\dfrac{110\cdot4+130\cdot15+150\cdot14+170\cdot5+190\cdot2}{40}=143\)
- Trung vị là: \(M_e=140+\left(\dfrac{20-19}{14}\right)\cdot20\simeq141\)
- \(Q_1=120+\left(\dfrac{10-4}{15}\right)\cdot20\simeq128\\ Q_2=M_e\simeq141\\ Q_3=140+\left(\dfrac{30-19}{15}\right)\cdot20=155,6\)
c, Mốt của mẫu số liệu là:
Có nhóm 2 là nhóm có tần số lớn nhất
\(\Rightarrow M_o=120+\left(\dfrac{15-4}{2\cdot15-4-14}\right)\cdot20\simeq138,3\)