M=1-2-2 ^2 -2 ^3 -2 ^ 4 .......-2^ 100. Giúp mik vs ạ,please

K

Khách

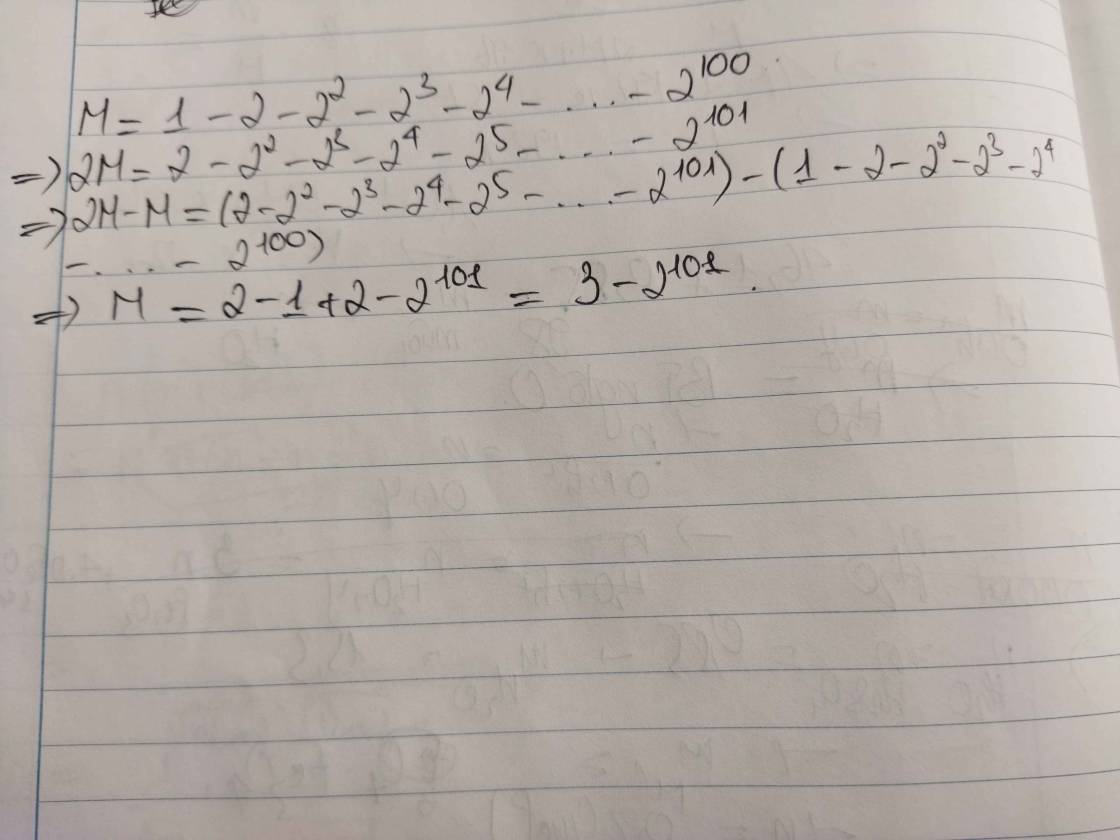
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

DH

dia hinamori

27 tháng 12 2023 - olm

M=1-2-2 ^2 -2 ^3 -2 ^ 4 .......-2^ 100.

Giúp mik vs ạ,please

1

DT

Dang Tung

CTVHS

27 tháng 12 2023

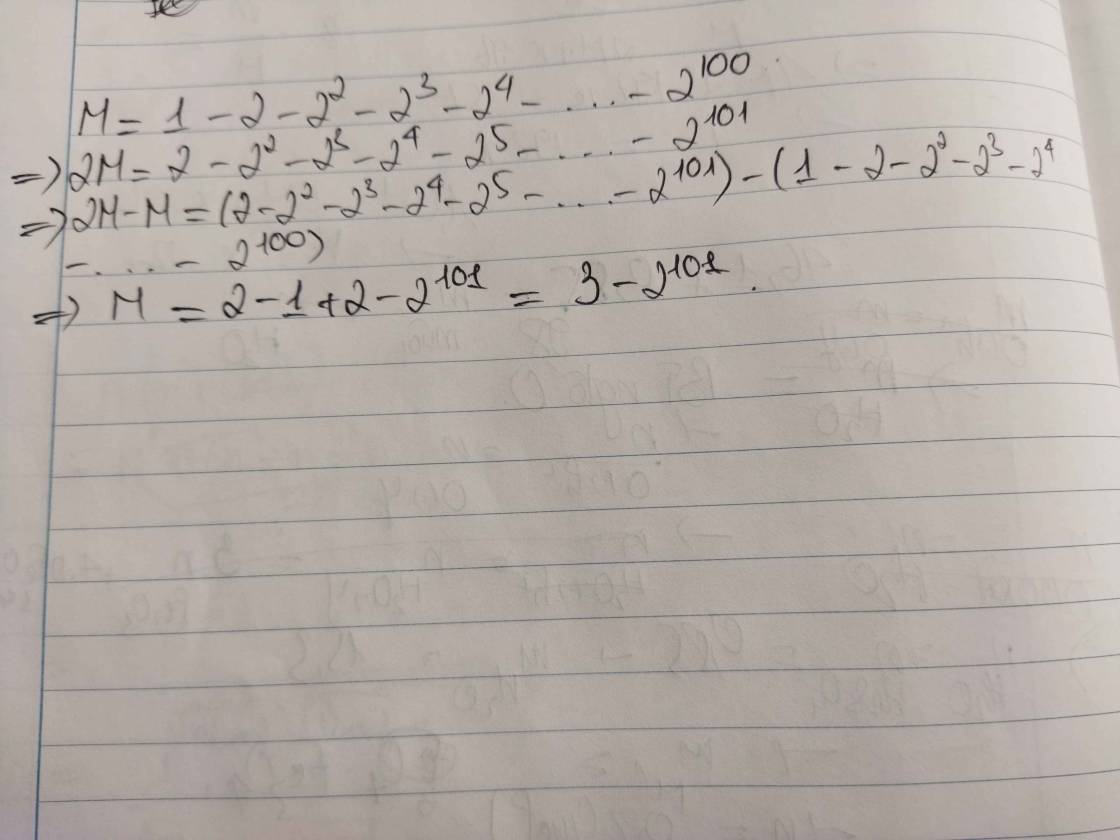
loading...

Các câu hỏi dưới đây có thể giống với câu hỏi trên

KC

kikei chimi

8 tháng 7 2015 - olm

tính giá trị của:

a, M=100^2-99^2+98^2-97^2+...+2^2-1^2

b, B=(20^2+18^2+16^2+...+4^2+2^2)-(19^2+17^2+15^2+...+3^2+1^2)

giúp mik vs nha

0

K

Khanhmy

29 tháng 11 2019 - olm

Tìm x biết

2/7x + 1/2 = -3/4

( 6x + 2/5 ) = -8/125

| x - 2/3 | . ( 18 - 6x mũ 2 ) = 0

Giúp m với m cần gấp ạ please nhanh ạ

1

M

Me

29 tháng 11 2019

Bài giải

a, \(\frac{2}{7}x+\frac{1}{2}=-\frac{3}{4}\)

\(\frac{2}{7}x=-\frac{3}{4}-\frac{1}{2}\)

\(\frac{2}{7}x=-\frac{5}{4}\)

\(x=-\frac{5}{4}\text{ : }\frac{2}{7}\)

\(x=-\frac{35}{8}\)

b, \(\left(6x+\frac{2}{5}\right)=-\frac{8}{125}\)

\(6x=-\frac{8}{125}-\frac{2}{5}\)

\(6x=-\frac{58}{125}\)

\(x=-\frac{58}{125}\text{ : }6\)

\(x=\frac{-29}{375}\)

c, \(\left|x-\frac{2}{3}\right|\cdot\left(18-6x^2\right)=0\)

\(\Rightarrow\orbr{\begin{cases}\left|x-\frac{2}{3}\right|=0\\18-6x^2=0\end{cases}}\)\(\Rightarrow\orbr{\begin{cases}x-\frac{2}{3}=0\\6x^2=18\end{cases}}\)\(\Rightarrow\orbr{\begin{cases}x=\frac{2}{3}\\x^2=3\end{cases}}\)\(\Rightarrow\orbr{\begin{cases}x=\frac{2}{3}\\x=\sqrt{3}\end{cases}}\)

\(\Rightarrow\text{ }x\in\left\{\frac{2}{3}\text{ ; }\sqrt{3}\right\}\)

VN

Vũ Ngu Mạnh Ngốc

4 tháng 4 2018 - olm

tính tổng M=\(1+\frac{3}{2^3}+\frac{4}{2^4}+.....+\frac{100}{2^{100}}\)

giúp mình vs mình tick đúng cho

0

A

Anh

22 tháng 9 2019 - olm

CMR

1/2! + 2/3! + 3/4! +...+ 99/100! <1

Mn giúp m vs

1

NN

Nguyễn Ngọc Phương Anh (🍩 Team ☆ Fr...

22 tháng 9 2019

Bạn vào link này nè:https://olm.vn/hoi-dap/detail/55490238293.html?pos=83878663774

NM

Nguyen My Thuc

26 tháng 3 2017 - olm

1+ 1/2(1+2) + 1/3(1+2+3) +1/4(1+2+3+4) +....+1/100(1+2+3+..+100)

Ai giúp mk vs .....

3

HC

Hà Chí Dương

26 tháng 3 2017

Tk mình đi mọi người mình bị âm nè!

Ai tk mình mình tk lại cho

HC

Hà Chí Dương

26 tháng 3 2017

Tk mình đi mọi người mình bị âm nè!

Ai tk mình mình tk lại cho

TT

Trần Thế Tín

6 tháng 8 2020 - olm

tìm x biết ( 3/2 - 5/11 - 3/13 ) (2x - 2) = ( -3/4 + 5/22 +3/26)

giải giúp mik vs ạ

mik đang cần gấp cảm ơn trc ạ

1

XO

Xyz OLM

6 tháng 8 2020

Ta có :\(\left(\frac{3}{2}-\frac{5}{11}-\frac{3}{13}\right).\left(2x-2\right)=\left(-\frac{3}{4}+\frac{5}{22}+\frac{3}{26}\right)\)

=> \(\left(\frac{3}{2}-\frac{5}{11}-\frac{3}{13}\right).\left(2x-2\right)=-\frac{1}{2}\left(\frac{3}{2}-\frac{5}{11}-\frac{3}{13}\right)\)

=> \(2x-2=-\frac{1}{2}\)

=> \(2x=\frac{3}{2}\)

=> \(x=\frac{3}{4}\)

LN

Lê Ngọc Hà

30 tháng 9 2021 - olm

a)(3/10-4/15-7/20).5/19 / (1/14+1/7-(-3/35)).(-4/3)
b)(1+2+3+...+100).(1/3-1/5-1/7-1/9).(6,3.12-21.3,6) / 1/2+1/3+1/4+...+1/100
LÀM GIÚP MIK VỚI Ạ MIK GẤP LẮM RỒI

0

LN

La Na Ivy

2 tháng 2 2017 - olm

TÍNH a=1/2+2/2^2+3/2^3+4/2^4+...+100/2^100

LÀM ƠN GIÚP MK VS!!!!!!!!!!!!!!

Nay và Mai

3

D

dinhkhachoang

2 tháng 2 2017

ta có

A=1/2+2/2^2+3/2^3+4/2^4+.....+100/2^100

2A=2/2^2+2/2^3+2/2^4+.......+100/2^100

2A-A=1/2-100/2^100

=>A=1/2

CHẮC SAI ẤY MÀ

TV

Thái Vũ Đức Anh

2 tháng 2 2017

Bạn bấm đề lên google xem được không , không cần k cho mình đâu

NH

Nguyễn Hoài Hải Anh

23 tháng 4 2020 - olm

Giúp mik vs ak

Câu2

a) (x-2)^x+4=(x-2)^x.(x-2)^4

b) x.(x-1/3)<0

Giúp mik vs ak, mik đg cần gấp trc 7h tối ak. Ai làm đúng mik tick 2 cái ak

1

TL

Tran Le Khanh Linh

24 tháng 4 2020

\(x\left(x-\frac{1}{3}\right)< 0\)

Để \(x\left(x-\frac{1}{3}\right)< 0\)thì x và \(x-\frac{1}{3}\)trái dấu nhau

Thấy \(x>x-\frac{1}{3}\)\(\Rightarrow\hept{\begin{cases}x>0\\x-\frac{1}{3}< 0\end{cases}\Rightarrow\hept{\begin{cases}x>0\\x< \frac{1}{3}\end{cases}\Leftrightarrow}0< x< \frac{1}{3}}\)