Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tại những điểm cách O một đoạn x thì biên độ giảm \(2.5\sqrt{x}\)lần
=> biên độ tại điểm M cách O một đoạn 25cm là \(\frac{2}{2,5.\sqrt{25}} = 0.16cm. \)
M trễ pha hơn O:
\(u_M=0.16\cos(4\pi t - 2\pi\frac{OM}{\lambda})= 0.16\cos(40\pi t - \frac{5\pi}{3})cm.\)

\(u_M= 5\cos(4\pi t - 2 \pi \frac{d}{\lambda}) = 5\cos(4\pi t - 2 \pi \frac{50}{20})=5\cos(4\pi t - 5 \pi) cm.\)

Đáp án B
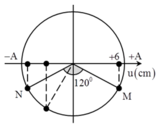
+ Độ lệch pha giữa M và N:
∆ φ MN = 2 π ∆ x MN λ = 2 π 3 rad .
+ Biễu diễn các vị trí tương ứng của M và N trên đường tròn tại thời điểm t
⇒ A = 4 3 cm
+ Khi M đến biên thì u N = - A 2 = - 2 3 cm .

Hướng dẫn: Chọn đáp án A
Thời gian cần thiết sóng truyền từ O đến M: 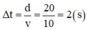
* Khi t = 1,5 s thì sóng chưa truyền đến M nên uM = 0.
* Khi t = 2,5 s thì sóng đã truyền đến rồi, để tìm li độ ta viết phương trình sóng tại M:
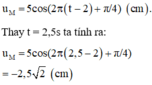
Chú ý: Khi cho biết phương trình sóng u = a cos ω t ∓ 2 π λ x

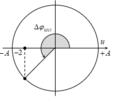
+ Độ lệch pha giữa hai điểm M và O là
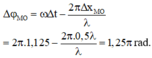
→ Biểu diễn dao động của điểm O và M tương ứng trên đường tròn. Tại thời điểm ban đầu điểm O đang ở vị trí biên dương.
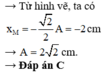


Bước sóng: \(\lambda=\frac{v}{f}=\frac{20}{5}=4cm\)
Theo giả thiết, ta có M sớm pha hơn N là: \(\Delta\varphi=\frac{2\pi\left(d_2-d_1\right)}{\lambda}=\frac{2\pi\left(20-5\right)}{4}=\frac{15}{2}\pi\)(rad)
Do M, N đều là những dao động điều hòa cùng tần số, nên ta biểu diễn dao động trên véc tơ quay như sau:
Li độ \(u_N\) chính là tọa độ của N trên trục 0u.
Nhìn vào hình vẽ ta có: \(\left|u_N\right|=\sqrt{5^2-4^2}=3cm\)
Vì \(u_N\) ở li độ âm nên li độ của N là: -3cm.