Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi khoảng cách giữa hai bến A và B là x ( km), ĐK: x > 0 .
Khi đó: Vận tốc của ca nô đi từ A đến B là : \(\frac{x}{5}\)(km/h)
Vận tốc của ca nô đi từ B đến A là : \(\frac{x}{7}\) (km/h)
Theo đề ra ta có phương trình: 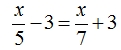
Giải phương trình và đến kết quả x = 105 ( thoả mãn)
Vậy khoảng cách giữa hai bến A và B là 105 km.

Trả lời : Bài làm
Đổi :\(1h20p=\frac{4}{3}h\)
Vận tốc thực của cano là:30-5=25 (km/h)
Gọi x là độ dài từ A đến B
Thời gian cano xuôi dòng là:\(\frac{x}{25+5}h\)
Thời gian cano ngược dòng là: \(\frac{x}{25-5}h\)
Từ đó ta có pt: \(\frac{x}{20}-\frac{x}{30}=\frac{4}{3}\)
Giải ra được \(x=80km\)
Mk ko chắc
Tk mk nha

C1: Một canô ngược dòng từ bến A đến bến B với vận tốc 20 km/h, sau đó lại xuôi từ bến B trở về bến A. Thời gian canô ngược dòng từ A đến B nhiều hơn thời gian canô xuôi dòng từ B trở về A là 2 giờ 40 phút. Tính khoảng cách giữa hai bến A và B. Biết vận tốc dòng nước là 5 km/h, vận tốc riêng của canô lúc xuôi dòng và lúc ngược dòng bằng nhau.
Giải: 2 giờ 40 phút = \(\dfrac{8}{3}\) giờ.
Vận tốc thực của cano là: \(20+5=25\left(km/h\right).\)
Vận tốc cano đi xuôi dòng là: \(25+5=30\left(km/h\right).\)
Gọi thời gian cano đi xuôi dòng là: \(x\left(h\right);x>0.\)
\(\Rightarrow\) Thời gian cano đi ngược dòng là: \(x+\dfrac{8}{3}\left(h\right).\)
Quãng đường cano đi xuôi dòng là: \(30x\left(km\right).\)
Quãng đường cano đi ngược dòng là:
\(20\left(x+\dfrac{8}{3}\right)=20x+\dfrac{160}{3}\left(km\right).\)
Vì cano đi xuôi và ngược đều cùng trên 1 quãng đường nên ta có phương trình sau:
\(30x=20x+\dfrac{160}{3}.\\ \Leftrightarrow10x-\dfrac{160}{3}=0.\\ \Leftrightarrow x=\dfrac{16}{3}\left(TM\right).\)
\(\Rightarrow\) Khoảng cách giữa hai bến A và B là: \(30.\dfrac{16}{3}=160\left(km\right).\)

Gọi khoảng cách AB là x
Vận tốc thực ko đổi
=>Vận tốc từ B về A là 30km/h
Theo đề, ta có: x/33+x/27=2/3
=>x=99/10
Gọi khoảng cách giữa A và B là \(x\left(km\right)\)
Khi đó bạn sẽ có 2 phương trình theo đề bài:
Thời gian khi xuôi dòng từ A đến B là: \(t_1=\dfrac{x}{\left(30+3\right)}\)
Thời gian khi ngược dòng từ B về A là: \(t_2=\dfrac{x}{\left(30-3\right)}\)
Mà thời gian khi xuôi dòng ít hơn thời gian khi ngược dòng là \(\dfrac{2}{3}\) giờ
\(t_1+\dfrac{2}{3}=t_2\)
\(\Leftrightarrow\dfrac{x}{\left(30+3\right)}+\dfrac{2}{3}=\dfrac{x}{\left(30-3\right)}\)
\(\Leftrightarrow\dfrac{x}{33}+\dfrac{2}{3}=\dfrac{x}{27}\)
\(\Leftrightarrow\dfrac{x}{33}+\dfrac{22}{33}=\dfrac{x}{27}\)
\(\Leftrightarrow\dfrac{x+22}{33}=\dfrac{x}{27}\)
\(\Leftrightarrow27\left(x+22\right)=33x\)
\(\Leftrightarrow27x+594=33x\)
\(\Leftrightarrow594=33x-27x=6x\)
\(\Leftrightarrow x=\dfrac{594}{6}=99\left(km\right)\)
Vậy quãng đường AB có độ dài 99km

Gọi vận tốc thực của cano là x(km/h;x>4)
vận tốc xuôi dòng của cano là x+4(km/h)
=> thời gian xuôi dòng của cano là 30/(x+4) (h)
vận tốc ngược dòng của cano là x-4(km/h)
=> thời gian tốc ngược dòng của cano là 30/(x-4) (h)
mà thời gian đi lẫn về của cano là 4 h
=> 30/(x+4)+30/(x-4)=4(chỗ này bạn giải được)
<=> x = 16 và x=-1(loại)
=> vận tốc thực của cano là 16km/h
vậy vận tốc thực của cano là 16km/h

Gọi vận tốc thực của cano là x
\(\Rightarrow\) Vận tốc cano khi xuôi dòng là x+2 \(\Rightarrow\) Thời gian xuôi dòng là \(\frac{120}{x+2}\)
Vân tốc cano khi ngược dòng là \(x-2\Rightarrow\)Thời gian ngược dòng là \(\frac{120}{x-2}\)
Mà thời gian cano xuôi ít(sửa đề) hơn thời gian ngược là 1 giờ
\(\Rightarrow\frac{120}{x+2}+1=\frac{120}{x-2}\)
\(\Rightarrow120\left(x-2\right)+\left(x+2\right)\left(x-2\right)=120\left(x+2\right)\)
\(\Rightarrow x^2+120x-244=120x+240\)
\(\Rightarrow x^2=484\)
\(\Rightarrow x=22\) vì x > 0

Gọi vận tốc ca nô là x (x >2)
vận tốc ca nô khi xuôi dòng : x + 2
vận tốc ca nô khi ngược dòng : x - 2
ta có \(S=4\left(x+2\right)=5\left(x-2\right).\)
\(\Leftrightarrow4x+8=5x-10\)
\(\Leftrightarrow x=18\)
\(\Rightarrow S=4\left(x+2\right)=4\left(18+2\right)=80\)(km)