TN
9
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
0
PT
3
11 tháng 3 2022
theo mình thì câu trên: dưới mẫu trong căn bỏ n^2 ra làm nhân tử chung xong đặt nhân tử chung của cả mẫu là n^2 . câu dưới thì mình k biết!!
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 3 2022
\(\lim\dfrac{-3n+2}{n-\sqrt{4n+n^2}}=\lim\dfrac{\left(-3n+2\right)\left(n+\sqrt{4n+n^2}\right)}{\left(n-\sqrt{4n+n^2}\right)\left(n+\sqrt{4n+n^2}\right)}\)
\(=\lim\dfrac{\left(-3n+2\right)\left(n+\sqrt{4n+n^2}\right)}{-4n}=\lim\dfrac{n\left(-3+\dfrac{2}{n}\right)n\left(1+\sqrt{\dfrac{4}{n}+1}\right)}{-4n}\)
\(=\lim n\dfrac{\left(-3+\dfrac{2}{n}\right)\left(1+\sqrt{\dfrac{4}{n}+1}\right)}{-4}\)
Do \(\lim\left(n\right)=+\infty\)
\(\lim\dfrac{\left(-3+\dfrac{2}{n}\right)\left(1+\sqrt{\dfrac{4}{n}+1}\right)}{-4}=\dfrac{\left(-3+0\right)\left(1+\sqrt{0+1}\right)}{-4}=\dfrac{3}{2}>0\)
\(\Rightarrow\lim n\dfrac{\left(-3+\dfrac{2}{n}\right)\left(1+\sqrt{\dfrac{4}{n}+1}\right)}{-4}=+\infty\)
TG
mọi người giải giúp em theo phương pháp tự luận với ạ
2
22 tháng 8 2021
Câu 1: Ý C
PT \(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\cosx=\dfrac{\sqrt{3}}{2}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\) mà\(x\in\left(0;2\pi\right)\)
Có 3 nghiệm
Câu 2: Ý A
PT \(\Leftrightarrow\left[{}\begin{matrix}sinx=1\\sinx=\dfrac{1}{2}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k2\pi\\x=\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\) mà \(0\le x< \dfrac{\pi}{2}\)
\(\Rightarrow x=\dfrac{\pi}{6}\)
KB
8 tháng 4 2022
2.B (t/c của giới hạn)
6.B H/s ko x/đ với x = 0 -> Ko liên tục tại đ x = 0
17.C
24. \(\lim\limits_{x\rightarrow\left(-1\right)^-}\dfrac{2x+1}{x+1}\) . Thấy : \(\lim\limits_{x\rightarrow\left(-1\right)^-}2x+1=2.\left(-1\right)+1=-1\)
\(\lim\limits_{x\rightarrow\left(-1\right)^-}x+1=0\) ; \(x\rightarrow\left(-1\right)^-\Rightarrow x+1< 0\).
Do đó : \(\lim\limits_{x\rightarrow\left(-1\right)^-}=+\infty\) . Chọn B
KB
8 tháng 4 2022
33 . B
Trên (SAB) ; Lấy H là TĐ của AB ; ta có : SH \(\perp AB\) ( \(\Delta SAB\) đều ) ; HC \(\perp AB\) ( \(\Delta ABC\) đều )
Ta có : (SAB) \(\perp\left(ABC\right)\) ; \(\left(SAB\right)\cap\left(ABC\right)=AB;SH\perp AB\)
\(\Rightarrow SH\perp\left(ABC\right)\)
\(SC\cap\left(ABC\right)=C\) . Suy ra : \(\left(SC;\left(ABC\right)\right)=\widehat{SCH}\)
Có : \(SH\perp HC\) => \(\Delta SHC\) vuông tại H
G/s \(\Delta\)ABC đều có cạnh là a \(\Rightarrow AB=a\)
\(\Delta SAB\) đều => SA = SB = AB = a
Tính được : \(SH=HC=\dfrac{\sqrt{3}}{2}a\)
\(\Delta SHC\) vuông tại H : \(tan\widehat{SCH}=\dfrac{SH}{HC}=1\)
\(\Rightarrow\widehat{SCH}=45^o\) => ...
MT
2
26 tháng 8 2021
Khoảng cách từ M để ABC bằng MA
Khoảng cách từ EF đến SAB bằng EM = AF
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 3 2022
1.a
\(\lim\dfrac{3n^3+2n^2+n}{n^3+4}=\lim\dfrac{n^3\left(3+\dfrac{2}{n}+\dfrac{1}{n^2}\right)}{n^3\left(1+\dfrac{4}{n^3}\right)}\)
\(=\lim\dfrac{3+\dfrac{2}{n}+\dfrac{1}{n^2}}{1+\dfrac{4}{n^3}}=\dfrac{3+0+0}{1+0}=3\)
b.
\(\lim\limits_{x\rightarrow3}\dfrac{x^2+2x-15}{x-3}=\lim\limits_{x\rightarrow3}\dfrac{\left(x-3\right)\left(x+5\right)}{x-3}\)
\(=\lim\limits_{x\rightarrow3}\left(x+5\right)=8\)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 3 2022
2.
Ta có:
\(\lim\limits_{x\rightarrow5}f\left(x\right)=\lim\limits_{x\rightarrow5}\dfrac{x^2-25}{x-5}=\lim\limits_{x\rightarrow5}\dfrac{\left(x-5\right)\left(x+5\right)}{x-5}\)
\(=\lim\limits_{x\rightarrow5}\left(x+5\right)=10\)
Và: \(f\left(5\right)=9\)
\(\Rightarrow\lim\limits_{x\rightarrow5}f\left(x\right)\ne f\left(5\right)\)
\(\Rightarrow\) Hàm gián đoạn tại \(x_0=5\)
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 3 2022
24.
\(\lim\limits_{x\rightarrow1}f\left(x\right)=\lim\limits_{x\rightarrow1}\dfrac{\sqrt{x}-1}{x-1}=\lim\limits_{x\rightarrow1}\dfrac{\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{1}{\sqrt{x}+1}=\dfrac{1}{1+1}=\dfrac{1}{2}\)
Hàm liên tục tại \(x=1\) khi:
\(\lim\limits_{x\rightarrow1}f\left(x\right)=f\left(1\right)\Rightarrow\dfrac{1}{2}=k+1\)
\(\Rightarrow k=-\dfrac{1}{2}\)
25.
\(S=\dfrac{u_1}{1-q}=\dfrac{1}{1-\left(-\dfrac{1}{2}\right)}=\dfrac{2}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 3 2022
26.
\(\overrightarrow{AD}=\overrightarrow{B'C'}\) nên \(\overrightarrow{AD}\) cùng hướng với \(\overrightarrow{B'C'}\)
27.
\(cos\left(\overrightarrow{a};\overrightarrow{b}\right)=\dfrac{\overrightarrow{a}.\overrightarrow{b}}{\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|}\)
\(\Rightarrow\overrightarrow{a}.\overrightarrow{b}=\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|.cos\left(\overrightarrow{a};\overrightarrow{b}\right)=3.5.cos120^0=-\dfrac{15}{2}\)
28.
Cả 4 khẳng định này đều sai
Khẳng định đúng: \(\overrightarrow{OA}+\overrightarrow{OC'}=\overrightarrow{0}\)
29.
\(\overrightarrow{MD}+\overrightarrow{MC}=\overrightarrow{0}\) là khẳng định đúng
DT
10 tháng 3 2022
Câu 31 B
Nếu đường thẳng \(\alpha\) song song với mặt phẳng (P) thì có duy nhất một mặt phẳng chứa 
và song song với (P).
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 10 2019
Bạn ghi sai đề thì phải
Cái mẫu đầu tiên có vấn đề, nếu (x-2) không có giai thừa thì pt này không thể giải được
BN
24 tháng 10 2019
à đúng rồi ạ, em xin lỗi ạ :)) ! ở chỗ đó có giai thừa ạ !
Anh giải giúp em vs ạ
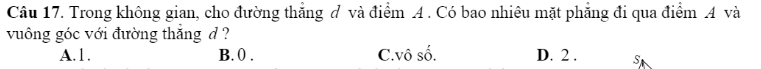
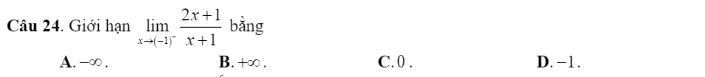
Câu 34:
\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}\left(x^2+3x-5\right)=5\)
\(\lim\limits_{x\rightarrow2^-}f\left(x\right)=\lim\limits_{x\rightarrow2^-}2=2\)
\(\Rightarrow\lim\limits_{x\rightarrow2^+}f\left(x\right)\ne\lim\limits_{x\rightarrow2^-}f\left(x\right)\)
\(\Rightarrow\) Không tồn tại giới hạn của hàm số khi \(x\rightarrow2\)
35.
\(\lim\limits_{x\rightarrow0}\frac{x\left(1-2cos^2x\right)}{sin2x}=\lim\limits_{x\rightarrow0}\frac{1-2cos^2x}{2.\left(\frac{sin2x}{2x}\right)}=\frac{1-2.1}{2.1}=-\frac{1}{2}\)
36.
Đáp án D đúng
Câu 24:
\(\lim\limits_{x\rightarrow2^-}\left[\frac{1}{\left(x-2\right)\left(x-3\right)}-\frac{1}{x-2}\right]=\lim\limits_{x\rightarrow2^-}\left[\frac{1-\left(x-3\right)}{\left(x-2\right)\left(x-3\right)}\right]\)
\(=\lim\limits_{x\rightarrow2^-}\frac{4-x}{\left(x-2\right)\left(x-3\right)}=\lim\limits_{x\rightarrow2^-}\frac{4-x}{\left(2-x\right)\left(3-x\right)}=\frac{2}{0}=+\infty\)
Câu 25:
\(\lim\limits_{x\rightarrow-\infty}\left[\sqrt{x^2+5x}+\sqrt{x^2+8}\right]\)
\(=\lim\limits_{x\rightarrow-\infty}\left[\left|x\right|\left(\sqrt{1+\frac{5}{x}}+\sqrt{1+\frac{8}{x^2}}\right)\right]=+\infty.\left(1+1\right)=+\infty\)
Câu 26:
\(\lim\limits_{x\rightarrow+\infty}\frac{\left(2x+5\right)^3\left(2-x\right)^4}{x^7+1}=\lim\limits_{x\rightarrow+\infty}\frac{x^3\left(2+\frac{5}{x}\right)^3.x^4\left(\frac{2}{x}-1\right)^4}{x^7\left(1+\frac{1}{x^7}\right)}\)
\(=\lim\limits_{x\rightarrow+\infty}\frac{\left(2+\frac{5}{x}\right)^3\left(\frac{2}{x}-1\right)^4}{1+\frac{1}{x^7}}=\frac{2^3.\left(-1\right)^4}{1}=8\)
Câu 27:
\(\lim\limits_{x\rightarrow3}\frac{\sqrt{2x+3}-3+3-\sqrt[3]{7x+6}}{x-3}=\lim\limits_{x\rightarrow3}\frac{\frac{2\left(x-3\right)}{\sqrt{2x+3}+3}-\frac{7\left(x-3\right)}{9+3\sqrt[3]{7x+6}+\sqrt[3]{\left(7x+6\right)^2}}}{x-3}\)
\(=\lim\limits_{x\rightarrow3}\left(\frac{2}{\sqrt{2x+3}+3}-\frac{7}{9+3\sqrt[3]{7x+6}+\sqrt[3]{\left(7x+6\right)^2}}\right)=\frac{2}{3+3}-\frac{7}{9+9+9}=\frac{2}{27}\)