Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
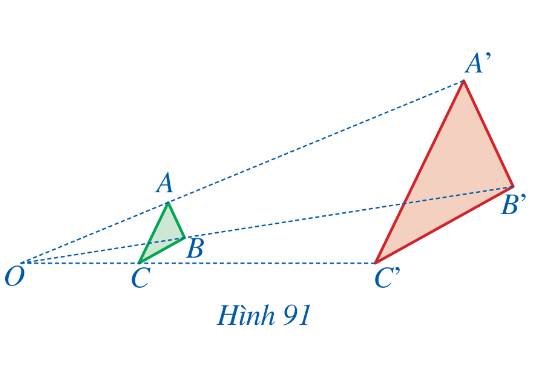
i) Vì \(OA' = 3OA \Rightarrow \frac{{OA}}{{OA'}} = \frac{1}{3}\);\(OB' = 3OB \Rightarrow \frac{{OB}}{{OB'}} = \frac{1}{3}\).
Xét tam giác \(OA'B'\) có:
\(\frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{1}{3}\)
Do đó, \(A'B'//AB\) (định lí Thales đảo)
ii) Vì \(A'B'//AB \Rightarrow \frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{{AB}}{{A'B'}} = \frac{1}{3}\) (hệ quả của định lí Thales)
Do đó, \(\frac{{A'B'}}{{AB}} = \frac{3}{1} = 3\).
b)
i)
- Vì \(OA' = 3OA \Rightarrow \frac{{OA}}{{OA'}} = \frac{1}{3}\);\(OB' = 3OB \Rightarrow \frac{{OB}}{{OB'}} = \frac{1}{3}\).
Xét tam giác \(OA'B'\) có:
\(\frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{1}{3}\)
Do đó, \(A'B'//AB\) (định lí Thales đảo)
Vì \(A'B'//AB \Rightarrow \frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{{AB}}{{A'B'}} = \frac{1}{3}\) (hệ quả của định lí Thales)
Do đó, \(\frac{{A'B'}}{{AB}} = \frac{3}{1} = 3\).
- Vì \(OA' = 3OA \Rightarrow \frac{{OA}}{{OA'}} = \frac{1}{3}\);\(OC' = 3OC \Rightarrow \frac{{OC}}{{OC'}} = \frac{1}{3}\).
Xét tam giác \(OA'C'\) có:
\(\frac{{OA}}{{OA'}} = \frac{{OC}}{{OC'}} = \frac{1}{3}\)
Do đó, \(A'C'//AC\) (định lí Thales đảo)
Vì \(A'C'//AC \Rightarrow \frac{{OA}}{{OA'}} = \frac{{OC}}{{OC'}} = \frac{{AC}}{{A'C'}} = \frac{1}{3}\) (hệ quả của định lí Thales)
Do đó, \(\frac{{A'C'}}{{AC}} = \frac{3}{1} = 3\).
- Vì \(OB' = 3OB \Rightarrow \frac{{OB}}{{OB'}} = \frac{1}{3}\);\(OC' = 3OC \Rightarrow \frac{{OC}}{{OC'}} = \frac{1}{3}\).
Xét tam giác \(OB'C'\) có:
\(\frac{{OB}}{{OB'}} = \frac{{OC}}{{OC'}} = \frac{1}{3}\)
Do đó, \(B'C'//BC\) (định lí Thales đảo)
Vì \(B'C'//BC \Rightarrow \frac{{OB}}{{OB'}} = \frac{{OC}}{{OC'}} = \frac{{BC}}{{B'C'}} = \frac{1}{3}\) (hệ quả của định lí Thales)
Do đó, \(\frac{{B'C'}}{{BC}} = \frac{3}{1} = 3\).
Do đó, \(\frac{{B'C'}}{{BC}} = \frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\)
ii) Xét tam giác \(A'B'C'\) và tam giác \(ABC\) ta có:
\(\frac{{B'C'}}{{BC}} = \frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\) (chứng minh trên)
Do đó, tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\).

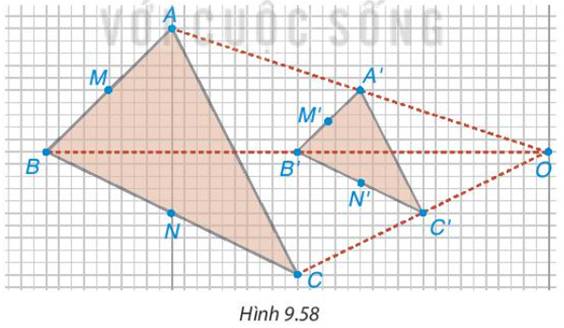
Từ điểm O, ‘‘phóng to’’ ba lần tam giác ABC, ta sẽ nhận được tam giác A’B’C’.

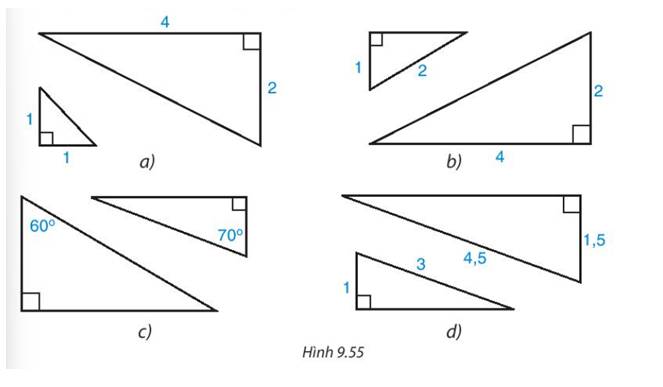
Cặp tam giác vuông ở hình d. Vì cạnh huyền và một cạnh góc vuông của tam giác này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia

- Vì \(OA' = 2OA \Rightarrow \frac{{OA}}{{OA'}} = \frac{1}{2}\);\(OB' = 2OB \Rightarrow \frac{{OB}}{{OB'}} = \frac{1}{2}\).
Xét tam giác \(OA'B'\) có:
\(\frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{1}{2}\)
Do đó, \(A'B'//AB\) (định lí Thales đảo)
Vì \(A'B'//AB \Rightarrow \frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{{AB}}{{A'B'}} = \frac{1}{2}\) (hệ quả của định lí Thales)
Do đó, \(\frac{{A'B'}}{{AB}} = \frac{2}{1} = 2\).
- Vì \(OA' = 3OA \Rightarrow \frac{{OA}}{{OA'}} = \frac{1}{3}\);\(OD' = 2OD \Rightarrow \frac{{OD}}{{OD'}} = \frac{1}{2}\).
Xét tam giác \(OA'D'\) có:
\(\frac{{OA}}{{OA'}} = \frac{{OD}}{{OD'}} = \frac{1}{2}\)
Do đó, \(A'D'//AD\) (định lí Thales đảo)
Vì \(A'D'//AD \Rightarrow \frac{{OA}}{{OA'}} = \frac{{OD}}{{OD'}} = \frac{{AD}}{{A'D'}} = \frac{1}{2}\) (hệ quả của định lí Thales)
Do đó, \(\frac{{A'D'}}{{AD}} = \frac{2}{1} = 2\).
- Vì \(OB' = 2OB \Rightarrow \frac{{OB}}{{OB'}} = \frac{1}{2}\);\(OC' = 2OC \Rightarrow \frac{{OC}}{{OC'}} = \frac{1}{2}\).
Xét tam giác \(OB'C'\) có:
\(\frac{{OB}}{{OB'}} = \frac{{OC}}{{OC'}} = \frac{1}{2}\)
Do đó, \(B'C'//BC\) (định lí Thales đảo)
Vì \(B'C'//BC \Rightarrow \frac{{OB}}{{OB'}} = \frac{{OC}}{{OC'}} = \frac{{BC}}{{B'C'}} = \frac{1}{2}\) (hệ quả của định lí Thales)
Do đó, \(\frac{{B'C'}}{{BC}} = \frac{2}{1} = 2\).
- Vì \(OD' = 2OD \Rightarrow \frac{{OD}}{{OD'}} = \frac{1}{2}\);\(OC' = 2OC \Rightarrow \frac{{OC}}{{OC'}} = \frac{1}{2}\).
Xét tam giác \(OD'C'\) có:
\(\frac{{OD}}{{OD'}} = \frac{{OC}}{{OC'}} = \frac{1}{2}\)
Do đó, \(D'C'//DC\) (định lí Thales đảo)
Vì \(D'C'//DC \Rightarrow \frac{{OD}}{{OD'}} = \frac{{OC}}{{OC'}} = \frac{{DC}}{{D'C'}} = \frac{1}{2}\) (hệ quả của định lí Thales)
Do đó, \(\frac{{D'C'}}{{DC}} = \frac{2}{1} = 2\).
Do đó, \(\frac{{B'C'}}{{BC}} = \frac{{A'B'}}{{AB}} = \frac{{C'D'}}{{CD}} = \frac{{A'D'}}{{AD}}\).


- Có \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}} = \frac{1}{2}\), góc O chung
=> ΔOA'B' ∽ ΔOAB (c.g.c)
- Có \(\frac{{OC'}}{{OC}} = \frac{{OB'}}{{OB}} = \frac{1}{2}\), góc O chung
=> ΔOB'C' ∽ ΔOBC(c.g.c)
=> ΔABC ∽ ΔA'B'C' (c.g.c)
- Đường thẳng có đi qua O