HT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MT
27 tháng 12 2015
câu 1 bạn phân tích ra là a(a+1)(a+2)(a+3) là 4 số tự nhiên liên tiếp nên chia hết cho 24.
câu 2 bạn phân tích ra thành (a-2)(a-1)a(a+1)(a+2) là 5 số tự nhiên liên tiếp nên chia hết cho 120
bài 3 phân tích ra thành:(a-2)(a-1)a(3a-5) nhưng mình k biết nó chia hết cho 24 ở chỗ nào
27 tháng 11 2018
\(A=\frac{9a^5-ab^4-18a^4b+2b^5}{3a^2b^2+ab^4-6a^2b^3-2b^5}\)
\(=\frac{a\left(9a^4-b^4\right)-2b\left(9a^4-b^4\right)}{ab^2\left(3a^2+b^2\right)-2b^3\left(3a^2+b^2\right)}\)
\(=\frac{\left(9a^4-b^4\right)\left(a-2b\right)}{\left(3a^2+b^2\right)\left(ab^2-2b^3\right)}\)
\(=\frac{\left(3a^2-b^2\right)\left(3a^2+b^2\right)\left(a-2b\right)}{\left(3a^2+b^2\right)b^2\left(a-2b\right)}\)
\(=\frac{3a^2-b^2}{b^2}\)
\(=3.\left(\frac{a}{b}\right)^2-1=3.\left(\frac{2}{3}\right)^2-1=\frac{1}{3}\)
PM
1
31 tháng 10 2019
\(=27a^6-18a^4b^3+12a^2b^6-18a^4b^3+12a^2b^6-8b^9\)
\(=27a^6-36a^4b^3+24a^2b^6-8a^9\)
19 tháng 7 2016
\(\left(3x^2-26^3\right)\left(9a^4+6a^2b^3+4b^6\right)\)
giả sử bạn sử dụng hằng đẳng thức số 7 thì không làm được bởi vì vế thì nhất không có b vế thứ 2 có b làm sao mình làm được
NN
2
MP
11 tháng 9 2023
\(a.2a+4b+\left(-4b+5a\right)-\left(6a-9b\right)\)
\(=2a+4b-4b+5a-6a+9b\)
\(=\left(2a+5a-6a\right)+\left(4b-4b+9b\right)\)
\(=a+9b\)
\(b.6a\left[b+3a-\left(4a-b\right)\right]\)
\(=6a\left[b+3a-4a+b\right]\)
\(=6a\left[4a-a+b+b\right]\)
\(=6a\left(3a-2b\right)\)
TT
0
29 tháng 7 2019
a, = 3x2y3 : x2y2 - 5x2y2 : x2y2 +6x4y7 :x2y2 -9x5y4 :x2y2
= 3y -5+ x2y5 -9x3y2
b., = a2.(6a-3):a2 + 3a(4a+3):3a = 6a - 3+ 4a +3= 10a
QH
25 tháng 11 2017
a,\(\dfrac{9a^2-16b^2}{4b-3a}=\dfrac{\left(3a-4b\right)\left(3a+4b\right)}{\text{4b-3a}}=-3a-4b\)
b,\(\dfrac{25a^2-30ab+9b^2}{3b-5a}=\dfrac{\left(5a-3b\right)^2}{3b-5a}=3b-5a\)
c,\(\dfrac{27a^3-27a^2+9a-1}{9a^2-6a+1}=\dfrac{27a^3-9a^2-18a^2+6a+3a-1}{9a^2-6a+1}=\dfrac{\left(3a-1\right)\left(9a^2-6a+1\right)}{9a^2-6a+1}=3a-1\)
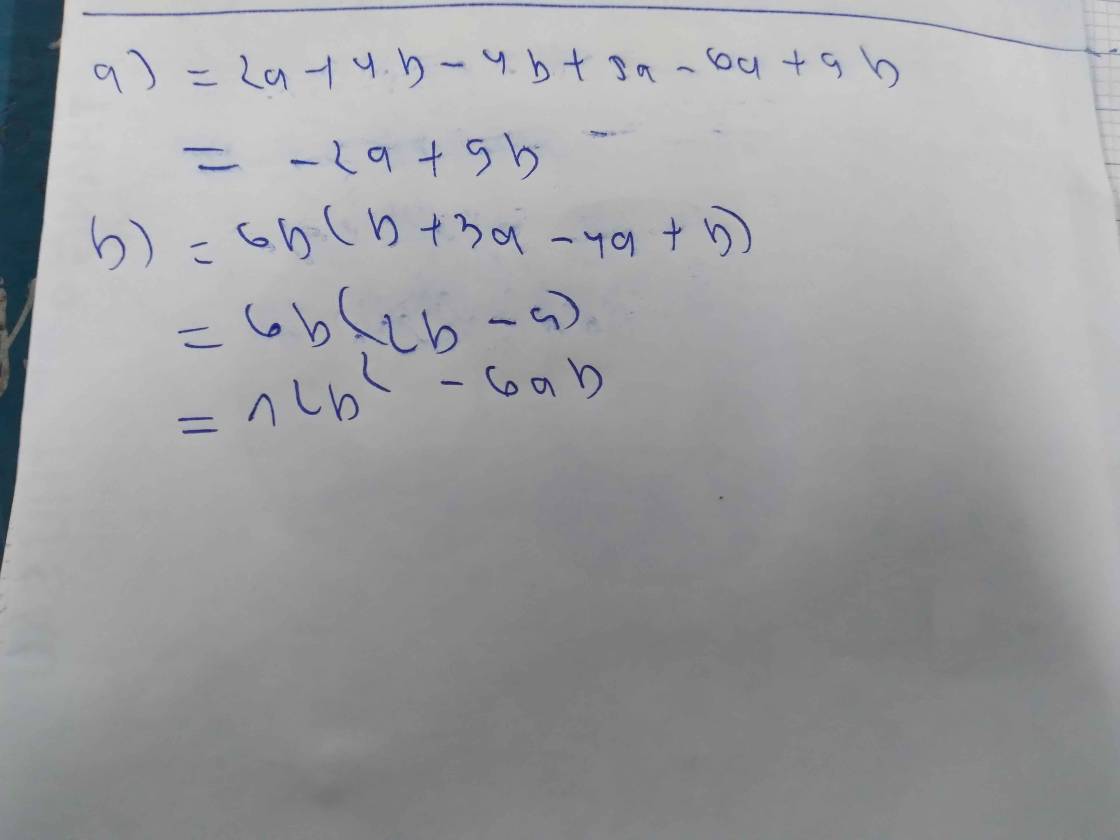
\(=\left(a^3-\dfrac{2}{3}a^4-a^3+\dfrac{3}{2}a^2\right)\cdot\left(\dfrac{3}{2}a^2+\dfrac{2}{3}a^4\right)\)
\(=\left(\dfrac{3}{2}a^2-\dfrac{2}{3}a^4\right)\left(\dfrac{3}{2}a^2+\dfrac{2}{3}a^4\right)\)
\(=\dfrac{9}{4}a^4-\dfrac{4}{9}a^8\)