Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vận tốc trung bình của vận động viên trong mỗi khoảng thời gian là:
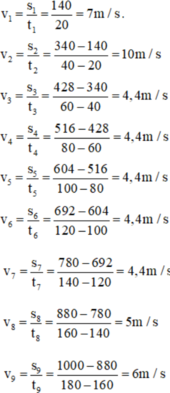
Dựa vào kết quả trên, ta thấy:
Trong hai quãng đường đầu: vận động viên chuyển động nhanh dần.
Trong năm quãng đường sau: vận động viên chuyển động đều.
Hai quãng đường sau cùng: vận động viên chuyển động nhanh dần.

1 Âm thanh truyền trong không kí với vận tốc 330m/s. Quãng đường âm thanh truyền đi được trong 0,5 phút là
a. 165m b. 11m c.660m d. 9,9km
2. Khi xe đang chuyển động, muốn cho xe dừng lại người ta dùng cái phanh ( thắng) xe để
a. tăng ma sát trượt b. tăng ma sát lăn
c. tăng ma sát nghỉ d.Cả a,b,c đều đúng
3. Tay ta cầm nắm được các vật là nhờ có
a. ma sát trượt b. ma sát lăn c. ma sát nghỉ d. quán tính
4. Có một ô tô đang chạy trên đường. Câu mô tả nào sau đây là đúng?
A. người điểu khiển ô tô đứng yên so với ô tô
B. người điển khiển mô tô đứng yên so với mặt đường
C. người điểu khiển mô tô đứng yên so với cột điện bên đường
D. người điều khiển mô tô chuyển động so với mô tô
4. làm thế nào để biết ai chạy nhanh, ai chạy chậm?
A. căn cứ vào thời gian chuyển động
B. căn cứ vào quãng đường mỗi người chạy được trong khoảng thời gian nhất định
C. căn cứ vào quãng đường và thời gian chuyển động
D. căn cứ vào quãng đường chuyển động
5. Trong các chuyển động sau, chuyển động nào là đều
A. chuyển động của quả dứa rơi từ trên cây xuống
B. chuyển động của Mặt Trăng quanh Trái Đất
C. chuyển động của đầu cánh quạt
D. chuyển động của xe buýt từ thủy phù lên Huế
6. Trong các chuyển động dưới đây chuyển động nào do tác dụng của trộng lực
A. xe đi trên đường B. thác nước đổ từ trên cao xuống
C. Mũi tên bắn ra từ cánh cung D. Quả bõng bị nảy lên khi chạm đất
7. mọt vật đang đứng yên trên mặt phẳng nằm ngang. Các lực tác dụng vào vật cân bằng nhau là
A. trọng lực P của Trái Đất với lực Ma sát F của mặt bàn
B. Trọng lực P của Trái Đất với lực đàn hồi
C. Trọng lực P của Trái Đất với phản lực N của mặt bàn
D. Lực ma sát F với phản lực N của mặt bàn
8. Một quả bóng khối lượng 1,5 kg được treo vào đầu một sợi dây, phải giữ đầu dây với một lực bằng bao nhiêu để quả bóng nằm cân bằng
A. 15N B. nhỏ hơn 1.5 N
C. 1.5 N D. nhỏ hơn 15N
9 trường hợp nào dưới đây xuất hiện lực ma sát lăn
A. Ma sát giữa má phanh và vành bánh xe khi phanh xe B. Ma sát giữa bánh xe với mặt đường
C. Ma sát tây cầm bóng D ma sát khi đánh diêm

Cứ 4 giây chuyển động thì ta gọi đó là một nhóm chuyển động
Thấy vận tốc của động tử trong các n nhóm chuyển động đầu tiên là: \(3^0m/s;3^1m/s;3^2m/s;3^3m/s;...;3^{n-1}m/s\)
Và quãng đường tương ứng của các nhóm đó là:
\(4.3^0m;4.3^1m;4.3^2m;4.3^3m;...;4.3^{n-1}m\)
Quãng đường động tử chuyển động trong thời gian là:
\(s_n=4\left(3^0+3^1+3^2+...+3^{n-1}\right)\)
\(K_n=3^0+3^1+3^2+3^3+....+3^{n-1}\)
\(\Rightarrow K_n+3^n=1+\left(1+3^1+3^2+...+3^{n-1}\right)=1+3K_n\)
\(K_n=\dfrac{3^n-1}{2}\)
\(\Rightarrow s_n=4.\left(\dfrac{3^n-1}{2}\right)=2\left(3^n-1\right)\)
Mà \(s_n=6km=6000m\)
\(\Rightarrow2\left(3^n-1\right)=6000\)
\(\Leftrightarrow3^n-1=\dfrac{6000}{2}\)
\(\Leftrightarrow3^n=2999\)
Ta có: \(3^6=729;3^7=2187;3^8=6561\Rightarrow n=7\)
Quãng đường động tử đi được trong 7 nhóm thời gian đầu tiên là:
\(2.2186=4372\left(m\right)\)
Quãng đường còn lại là:
\(6000-4372=1628\left(m\right)\)
Trong quãng đường còn lại này động tử đi với vận tốc là ( với n = 7):
\(3^7=2187m/s\)
Thời gian để đi hết quãng đường còn lại: \(\dfrac{1628}{2187}\approx0,74\left(s\right)\)
Tổng thời gian chuyển động của động tử: \(7.4+0,74=28,74\left(s\right)\)
Ngoài ra trong lúc chuyển động. động tử có ngừng 7 lần (không chuyển động) mỗi lần ngừng lại là 2 giây
Vậy thời gian cần để động tử chuyển động từ A tới B là:
\(28,74+2.7=42,74\left(s\right)\)

Gọi S1, S2 là quãng đường đi được của các vật,
v1,v2 là vận tốc vủa hai vật.
Ta có: S1 =v1t2 , S2= v2t2
Khi chuyển động lại gần nhau độ giảm khoảng cách của hai vật bằng tổng quãng đường hai vật đã đi: S1 + S2 = 8 m
S1 + S2 = (v1 + v2) t1 = 8
\(\Rightarrow\)v1 + v2 = \(\frac{S_1+S_2}{t_1}\) = \(\frac{5}{8}\) = 1,6 (1)
- Khi chúng chuyển động cùng chiều thì độ tăng khoảng cách giữa hai vật bằng hiệu quãng đường hai vật đã đi: S1 - S2 = 6 m
S1 - S2 = (v1 - v2) t2 = 6
\(\Rightarrow\)v1 - v2 = \(\frac{S_1-S_2}{t_1}\) = \(\frac{6}{10}\) = 0,6 (2)
Lấy (1) cộng (2) vế với vế ta được 2v1 = 2,2 \(\Leftrightarrow\)v1 = 1,1 m/s
Vận tốc vật thứ hai: v2 = 1,6 - 1,1 = 0,5 m/s
Bạn Lại Thị Hồng Liên làm ơn cho mình hỏi ngu xíu: có phải là:
- khi hai vật chuyển động ngược chiều thi độ TĂNG và cả GIẢM khoảng cách giữa hai vật đều bằng tổng quãng đường hai vật đi được
- khi chuyển động ngược chiều thì cả độ TĂNG hay GIẢM khoảng cách giữa hai vật đều bằng hiệu quãng đường hai vật đã đi?
Cảm ơn bạn nha!!!

Căn cứ vào thời gian chuyển động.