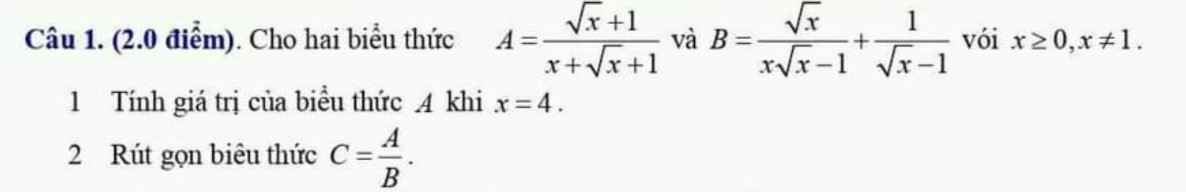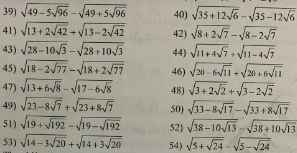K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
21 tháng 8 2021
2b)
xét vế trái ta có
=\(\left(\sqrt{x}-\sqrt{y}\right).\dfrac{\sqrt{x^2y}+\sqrt{xy^2}}{\sqrt{xy}}\) \(\left(\sqrt{x}-\sqrt{y}\right).\dfrac{\sqrt{xy}\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{xy}}\)=x-y
3b)
để A<0 \(\Rightarrow\dfrac{\sqrt{x}-1}{\sqrt{x}}< 0\)
\(\Rightarrow\sqrt{x}-1< 0\)\(\Rightarrow\sqrt{x}< 1\)\(\Rightarrow x< 1\)
21 tháng 8 2021
a: Ta có: \(\sqrt{9x^2-6x+1}=5\)
\(\Leftrightarrow\left|3x-1\right|=5\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=5\\3x-1=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=6\\3x=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-\dfrac{4}{3}\end{matrix}\right.\)
25 tháng 6 2021
15)
ĐKXĐ: \(x\ge1\)
Ta có: \(\sqrt{x+3}+\sqrt{x-1}=2\)
\(\Leftrightarrow2x+2+2\sqrt{\left(x+3\right)\left(x-1\right)}=4\)
\(\Leftrightarrow2\sqrt{\left(x+3\right)\left(x-1\right)}=2-2x\)
\(\Leftrightarrow\sqrt{\left(x+3\right)\left(x-1\right)}=1-x\)
\(\Leftrightarrow\left(x+3\right)\left(x-1\right)=\left(1-x\right)^2\)
\(\Leftrightarrow x^2-x+3x-3=x^2-2x+1\)
\(\Leftrightarrow2x-3+2x-1=0\)
\(\Leftrightarrow4x-4=0\)
\(\Leftrightarrow4x=4\)
hay x=1(thỏa ĐK)
Vậy: S={1}
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 2 2021
Kẻ đường kính AF, gọi G là trung điểm CF \(\Rightarrow\) G cố định. Nối GH cắt AN kéo dài tại J
ANCF nội tiếp \(\Rightarrow\widehat{ANC}+\widehat{AFC}=180^0\)
G và H là trung điểm các dây CF, CN \(\Rightarrow\left\{{}\begin{matrix}OH\perp CN\\OG\perp CF\end{matrix}\right.\)
\(\Rightarrow OHCG\) nội tiếp \(\Rightarrow\widehat{OHG}=\widehat{OCG}\) (cùng chắn OG)
Mà \(\widehat{OCG}=\widehat{AFC}\) (2 góc đáy tam giác OCF cân)
\(\Rightarrow\widehat{OHG}=\widehat{AFC}\Rightarrow\widehat{OHG}+\widehat{ANC}=180^0\)
Lại có \(\widehat{GHC}=\widehat{NHJ}\) (đối đỉnh), \(\widehat{OHG}+\widehat{GHC}=90^0\)
\(\Rightarrow\widehat{OHG}=90^0-\widehat{GHC}=90^0-\widehat{NHJ}\)
\(\Rightarrow\widehat{ANC}+90^0-\widehat{NHJ}=180^0\Rightarrow\widehat{ANC}-\widehat{NHJ}=90^0\)
\(\Leftrightarrow\widehat{NJH}+\widehat{NHJ}-\widehat{NHJ}=90^0\Leftrightarrow\widehat{NJH}=90^0\)
Hay \(GH\perp AN\)
Mà \(IH\perp AN\Rightarrow I\) trùng J hay G;H;I thẳng hàng
\(\Rightarrow\) IH luôn đi qua G cố định
Do I \(AI\perp IG\Rightarrow I\) luôn thuộc đường tròn đường kính AG cố định
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 2 2021
Theo tính chất 2 tiếp tuyến: \(\left\{{}\begin{matrix}AC=CM\\BD=DM\end{matrix}\right.\) \(\Rightarrow\dfrac{CM}{DM}=\dfrac{AC}{BD}\)
Mặt khác do AC//BD (cùng vuông góc AB)
\(\Rightarrow\dfrac{AC}{BD}=\dfrac{CN}{BN}\) (Talet) \(\Rightarrow\dfrac{CM}{DM}=\dfrac{CN}{BN}\Rightarrow MN||BD\)
Cũng theo Talet: \(\dfrac{CN}{BN}=\dfrac{AN}{DN}\Rightarrow\dfrac{BC}{BN}=\dfrac{AD}{DN}\Rightarrow\dfrac{BN}{BC}=\dfrac{ND}{AD}\) (1)
\(\dfrac{MN}{AC}=\dfrac{ND}{AD}\) ; \(\dfrac{NH}{AC}=\dfrac{BN}{BC}\) (2)
(1); (2) \(\Rightarrow\dfrac{MN}{AC}=\dfrac{NH}{AC}\Rightarrow MN=NH\)
2
19 tháng 5 2022
Với `x >= 0,x \ne 1` có:
`C=A/B=A:B=[\sqrt{x}+1]/[x+\sqrt{x}+1]:(\sqrt{x}/[x\sqrt{x}-1]+1/[\sqrt{x}-1])`
`C=[\sqrt{x}+1]/[x+\sqrt{x}+1]:[\sqrt{x}+x+\sqrt{x}+1]/[(\sqrt{x}-1)(x+\sqrt{x}+1)]`
`C=[\sqrt{x}+1]/[x+\sqrt{x}+1].[(\sqrt{x}-1)(x+\sqrt{x}+1)]/[x+2\sqrt{x}+1]`
`C=[\sqrt{x}+1]/[x+\sqrt{x}+1].[(\sqrt{x}-1)(x+\sqrt{x}+1)]/[(\sqrt{x}+1)^2]`
`C=[\sqrt{x}-1]/[\sqrt{x}+1]`
19 tháng 5 2022
1.Thế \(x=4\) vào A, ta được:
\(A=\dfrac{\sqrt{4}+1}{4+\sqrt{4}+1}=\dfrac{2+1}{4+2+1}=\dfrac{3}{7}\)
2.
\(B=\dfrac{\sqrt{x}}{x\sqrt{x}-1}+\dfrac{1}{\sqrt{x}-1}\)
\(B=\dfrac{\sqrt{x}}{\sqrt{x}^3-1}+\dfrac{1}{\sqrt{x}-1}\)
\(B=\dfrac{\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{1}{\sqrt{x}-1}\)
\(B=\dfrac{\sqrt{x}+\left(x+\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(B=\dfrac{x+2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(B=\dfrac{\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(C=\dfrac{A}{B}\)
\(C=\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}:\dfrac{\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(C=\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}.\dfrac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)^2}\)
\(C=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
TQ
14 tháng 6 2021
\(A=\dfrac{2\sqrt{x}+17}{\sqrt{x+5}}=\dfrac{2\sqrt{x}+10}{\sqrt{x}+5}+\dfrac{7}{\sqrt{x}+5}=2+\dfrac{7}{\sqrt{x}+5}\)
Để \(A\) ∈ \(Z\) thì \(\dfrac{7}{\sqrt{x}+5}\) phải ∈ \(Z\)
=> \(\sqrt{x}+5\) ∈ \(Ư\left(7\right)=\left\{-7;-1;1;7\right\}\)
# Với \(\sqrt{x}+5=-7=>\sqrt{x}=-12\)(Loại)
#Với \(\sqrt{x}+5=-1=>\sqrt{x}=-6\)(Loại)
#Với \(\sqrt{x}+5=1=>\sqrt{x}=-4\left(Loại\right)\)
#Với \(\sqrt{x}+5=7=>\sqrt{x}=2< =>x=4\left(Nhận\right)\)
Vậy \(x=4\) thì \(A\)∈\(Z\)
TQ
28 tháng 9 2021
\(\sqrt[3]{\dfrac{a^4}{b^2\left(a^2-ab+b^2\right)}}+\sqrt[3]{\dfrac{b^4}{c^2\left(b^2-bc+c^2\right)}}\sqrt[3]{\dfrac{c^4}{a^2\left(c^2-ac+b^2\right)}}\) \(\text{≥}3\)
\(Ta\) \(Có\) : \(\sqrt[3]{\dfrac{a^4}{b^2\left(a^2-ab+b^2\right)}}=\sqrt[3]{\dfrac{a^6}{ab.ab\left(a^2-ab+b^2\right)}}=\dfrac{a^2}{\sqrt[3]{ab.ab.\left(a^2-ab+b^2\right)}}\)
\(Áp\) \(dụng\) \(bđt\) \(AM-GM\)
\(\sqrt[3]{ab.ab\left(a^2-ab+b^2\right)}\text{≤}\) \(\dfrac{ab+ab+a^2-ab+b^2}{3}\)
\(=>\dfrac{a^2}{\sqrt[3]{ab.ab\left(a^2-ab+b^2\right)}}\) \(\text{≥}\) \(\dfrac{3a^2}{a^2+ab+b^2}\) \(Hay\) \(\sqrt[3]{\dfrac{a^4}{b^2\left(a^2-ab+b^2\right)}}\text{≥}\dfrac{3a^2}{a^2+ab+b^2}\)
Tương tự ta cũng có :
\(\sqrt[3]{\dfrac{b^4}{c^2\left(b^2-bc+c^2\right)}}\text{≥}\dfrac{3b^2}{b^2+bc+c^2}\)
\(\sqrt[3]{\dfrac{c^4}{a^2\left(c^2-ac+a^2\right)}}\text{≥}\dfrac{3c^2}{a^2+ac+c^2}\)
\(=>\text{}\text{}\)\(\sqrt[3]{\dfrac{a^4}{b^2\left(a^2-ab+b^2\right)}}+\sqrt[3]{\dfrac{b^4}{c^2\left(b^2-bc+c^2\right)}}\sqrt[3]{\dfrac{c^4}{a^2\left(c^2-ac+b^2\right)}}\) \(\text{≥}\) \(3\left(\dfrac{a^2}{a^2+ab+b^2}+\dfrac{b^2}{b^2+bc+c^2}+\dfrac{c^2}{a^2+ac+c^2}\right)\)
Cần c/m \(\left(\dfrac{a^2}{a^2+ab+b^2}+\dfrac{b^2}{b^2+bc+c^2}+\dfrac{c^2}{a^2+ac+c^2}\right)\) ≥ \(1\)
Ta có : \(\dfrac{a^2}{a^2+ab+b^2}\text{≥}\dfrac{1}{3}\)
\(< =>3a^2\text{≥}a^2+ab+b^2\) \(< =>2a^2-b\left(a+b\right)\text{≥}0\) (1)
Lại có : \(a^2\text{≥}-b\left(a+b\right)\) (2)
Từ (1) và (2) => \(\dfrac{a^2}{a^2+ab+b^2}\text{≥}\dfrac{1}{3}\)
Tương tự ta cũng có :
\(\dfrac{b^2}{b^2+bc+c^2}\text{≥}\dfrac{1}{3}\)
\(\dfrac{c^2}{a^2+ac+c^2}\text{≥}\dfrac{1}{3}\)
Do đó \(\dfrac{a^2}{a^2+ab+b^2}+\dfrac{b^2}{b^2+bc+c^2}+\dfrac{c^2}{a^2+ac+c^2}\text{≥}1\)
Suy ra : \(\sqrt[3]{\dfrac{a^4}{b^2\left(a^2-ab+b^2\right)}}+\sqrt[3]{\dfrac{b^4}{c^2\left(b^2-bc+c^2\right)}}\sqrt[3]{\dfrac{c^4}{a^2\left(c^2-ac+b^2\right)}}\) \(\text{≥}\) \(3\)
Đẳng thức xảy ra <=> \(a=b=c=1\)
1 tháng 8 2021
39) Ta có: \(\sqrt{49-5\sqrt{96}}-\sqrt{49+5\sqrt{96}}\)
\(=\sqrt{49-20\sqrt{6}}-\sqrt{49+20\sqrt{6}}\)
\(=5-2\sqrt{6}-5-2\sqrt{6}\)
\(=-4\sqrt{6}\)
40) Ta có: \(\sqrt{35+12\sqrt{6}}-\sqrt{35-12\sqrt{6}}\)
\(=3\sqrt{3}+2\sqrt{2}-3\sqrt{3}+2\sqrt{2}\)
\(=4\sqrt{2}\)
41) Ta có: \(\sqrt{13+2\sqrt{42}}+\sqrt{13-2\sqrt{42}}\)
\(=\sqrt{7}+\sqrt{6}+\sqrt{7}-\sqrt{6}\)
\(=2\sqrt{7}\)