
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


3. Xét tam giác ADM và tam giác AEM có :
góc ADM = góc AEM = 90 độ
Góc BAM = góc CAM (gt)
AM chung
=>Tam giác ADM = tam giác AEm (c.huyền - g.nhọn)
=>MD = ME (cặp cạnh t/ứng )
AD = AE (cặp cạnh t/ứng )
Xét tam giác MDB và tam giác MEC có :
MB = MC (gt)
góc MDB = góc MEC = 90 độ
MD = ME ( câu a)
=>Tam giác MDB = Tam giác MEC (c.huyền-c.g.vuông)
Vì AD + DB = AB
AE + EC = AC
Mà AD = AE
DB = EC
=>AB = AC
Xét tam giác ABM và tam giác ACM có
AM chung
góc BAM = góc CAM (gt)
AB = AC (CMT)
=>Tam giác ABM = Tam giác ACM (c.huyền-g.nhon)
Vậy có 3 cặp tam giác bằng nhau

a^+b^=c^
a^+b^+c^=180 độ
2a^=3b^
gõ hệ vào máy giải ra dc a^=54 ; b^=36;c^=90
mình chỉ bày cách để tính chứ ko phải cách làm đâu![]()
ta có A+B=C.Mà A+B+C=180 độ
Thay C+C=180 độ
=>2C=180 độ
=>c=90 độ hay A+B=90 độ
Ta có 2A=3B=>A/3=B/2=A+B/3+2=90/5=18
=>A=18.3=54
Vậy A=54


a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
BD=CE
\(\widehat{ABD}=\widehat{ACE}\)
Do đó: ΔABD=ΔACE
Suy ra: AB=AC
hay ΔABC cân tại A
b: XétΔABC có
AD là đường cao
CH là đường cao
AD cắt CH tại D
Do đó: D là trực tâm của ΔABC
=>BD vuông góc với AC

Vì x và y là hai đại lượng tỉ lệ thuận nên:
\(\frac{y_1}{x_1}=\frac{y_2}{x_2}\) = k (k \(\ne\) 0)
và \(x_1=6;x_2=-9\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{y_1}{x_1}=\frac{y_2}{x_2}=\frac{y_1-y_2}{x_1-x_2}=\frac{10}{6-\left(-9\right)}=\frac{10}{15}=\frac{2}{3}\)
\(\frac{y_1}{x_1}=\frac{2}{3}\Rightarrow y_1=\frac{2}{3}.x_1=\frac{2}{3}.6=4\)
\(\frac{y_2}{x_2}=\frac{2}{3}\Rightarrow y_2=\frac{2}{3}.x_2=\frac{2}{3}.\left(-9\right)=-6\)
Vậy: \(y_1+y_2=4+\left(-6\right)=-2\)


\(\frac{B}{A}=\frac{2^2+4^2+6^2+...+200^2}{1^2+2^2+...+100^2}=\frac{\left(1.2\right)^2+\left(2.2\right)^2+...+\left(100.2\right)^2}{1^2+2^2+...+100^2}\)
\(=\frac{1^2.2^2+2^2.2^2+...+100^2+2^2}{1^2+2^2+...+100^2}\)
\(=\frac{\left(1^2+2^2+...+100^2\right).2^2}{1^2+2^2+100^2}\)
\(=2^2=4\)
Vậy \(\frac{B}{A}=4\)
Sửa lại: ( tại nhìn bé quá, tưởng mũ 3 -> mũ 2 )
\(\frac{B}{A}=\frac{2^3+4^3+6^3+...+200^3}{1^3+2^3+...+100^3}\)
\(\Rightarrow\frac{B}{A}=\frac{\left(1.2\right)^3+\left(2.2\right)^3+...+\left(100.2\right)^3}{1^3+2^3+...+100^3}\)
\(\Rightarrow\frac{B}{A}=\frac{1^3.2^3+2^3.2^3+...+100^3.2^3}{1^3+2^3+...+100^3}\)
\(\Rightarrow\frac{B}{A}=\frac{\left(1^3+2^3+...+100^3\right)2^3}{1^3+2^3+...+100^3}\)
\(\Rightarrow\frac{B}{A}=2^3=8\)
Vậy \(\frac{B}{A}=8\)
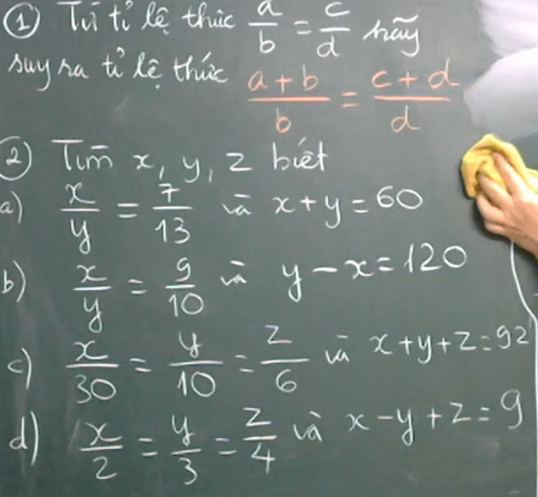

 M.n giải hộ em vs đg cần gấp ạ
M.n giải hộ em vs đg cần gấp ạ
 Làm hộ mình nha
Làm hộ mình nha








 Làm hộ mình với nhanh lên nha .Kết quả cũng được
Làm hộ mình với nhanh lên nha .Kết quả cũng được

Bài 2:
a) \(\dfrac{x}{y}=\dfrac{7}{13}\Rightarrow\dfrac{x}{7}=\dfrac{y}{13}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{7}=\dfrac{y}{13}=\dfrac{x+y}{7+13}=\dfrac{60}{20}=3\)
\(\dfrac{x}{7}=3\Rightarrow x=21\\ \dfrac{y}{13}=3\Rightarrow y=39\)
b) \(\dfrac{x}{y}=\dfrac{9}{10}\Rightarrow\dfrac{x}{9}=\dfrac{y}{10}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{9}=\dfrac{y}{10}=\dfrac{y-x}{10-9}=120\)
\(\dfrac{x}{9}=120\Rightarrow x=1080\\ \dfrac{y}{10}=120\Rightarrow y=1200\)
c) Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{30}=\dfrac{y}{10}=\dfrac{z}{6}=\dfrac{x+y+z}{30+10+6}=\dfrac{92}{46}=2\)
\(\dfrac{x}{30}=2\Rightarrow x=60\\ \dfrac{y}{10}=2\Rightarrow y=20\\ \dfrac{z}{6}=2\Rightarrow z=12\)
d)Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x-y+z}{2-3+4}=\dfrac{9}{3}=3\)
\(\dfrac{x}{2}=3\Rightarrow x=6\\ \dfrac{y}{3}=3\Rightarrow y=9\\ \dfrac{z}{4}=3\Rightarrow z=12\)
Bài 1:
\(\dfrac{a+b}{b}=\dfrac{a}{b}+1\)
\(\dfrac{c+d}{d}=\dfrac{c}{d}+1\)
Mà \(\dfrac{a}{b}=\dfrac{c}{d};1=1\Rightarrow\dfrac{a}{b}+1=\dfrac{c}{d}+1\Rightarrow\dfrac{a+b}{b}=\dfrac{c+d}{d}\)