
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2:
Ta có: \(3n^3+10n^2-5⋮3n+1\)
\(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow3n\in\left\{0;-3;3\right\}\)
hay \(n\in\left\{0;-1;1\right\}\)

Lời giải:
d.
Áp dụng định lý Menelaus cho tam giác $BDF$ có $A,O,M$ lần lượt thuộc $BD, DF, BF$ và $A,O,M$ thẳng hàng:
$\frac{MF}{MB}.\frac{OD}{OF}.\frac{AB}{AD}=1$
$\Leftrightarrow \frac{MF}{MB}.1.2=1$
$\Leftrightarrow \frac{MF}{MB}=\frac{1}{2}$
$\Rightarrow \frac{BF}{MB}=\frac{3}{2}$
$\Leftrightarrow \frac{BC}{2MB}=\frac{3}{2}$
$\Leftrightarrow BC=3MB$ (đpcm)

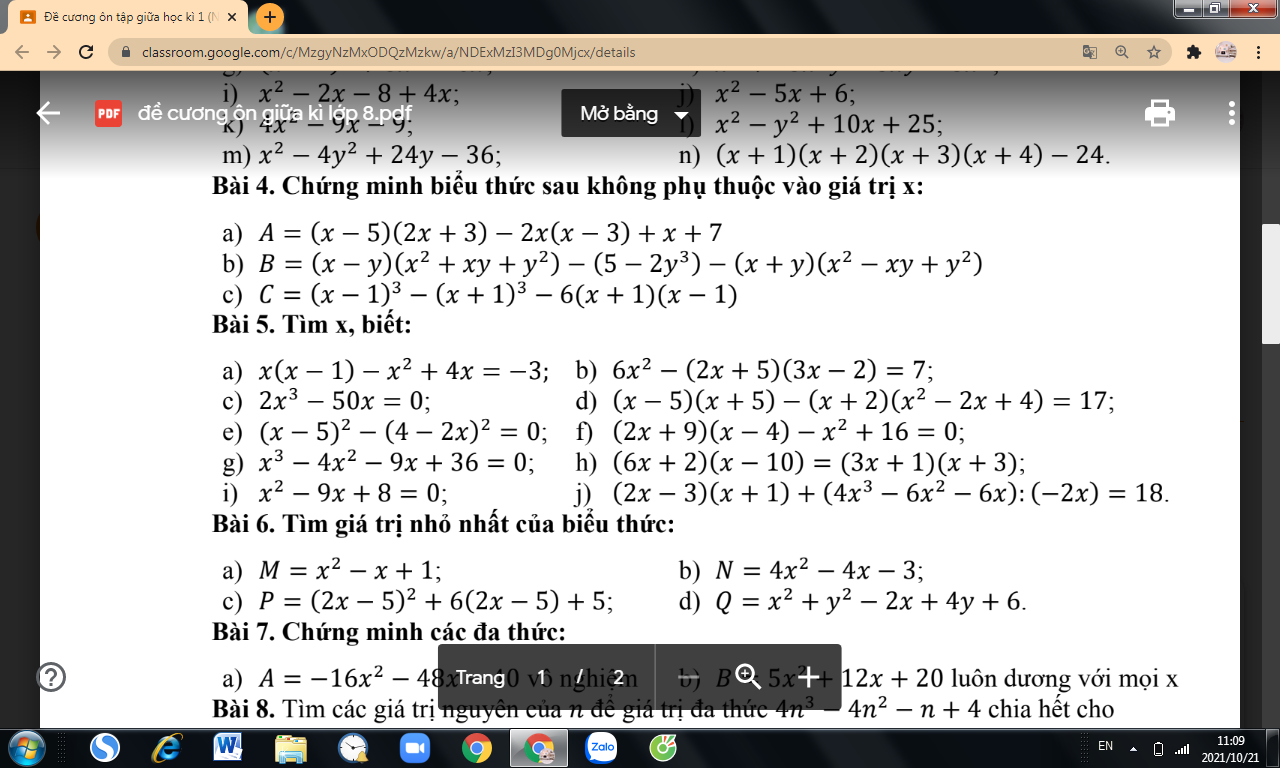
Bài 5:
i: \(x^2-9x+8=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-8\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=8\end{matrix}\right.\)

c: \(C=\sqrt{\left(a+5b\right)^2-20ab}=\sqrt{4^2+100}=4\sqrt{29}\)
d) D = a4 + 625b4
=> D = a4 + 20a3b + 150a2b2 + 500ab3 625b4 - (20a3b + 150a2b2 + 500ab3)
=> D = (a + 5b)4 - 5ab(4a2 + 40ab + 100b2 - 10ab)
=> D = (a + 5b)4 - 5ab[(2a + 10b)2 - 10ab]
=> D = (a + 5b)4 - 5ab[4(a + 5b)2 - 10ab]
=> D = 44 - 5 . (- 5)[4 . 42 - 10 . (- 5)]
=> D = 256 + 25(64 + 50)
=> D = 256 + 25 . 114
=> D = 256 + 2850 = 3106
Cái này mình dùng HĐT mở rộng bạn cóa thể tham khảo tam giác Pascal



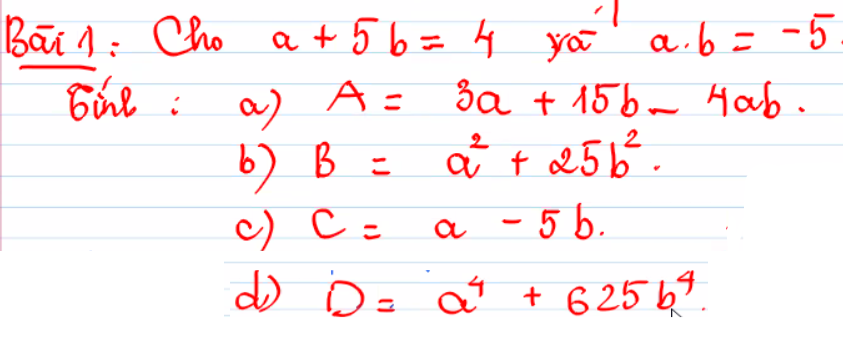

\(A=\frac{2\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\frac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}-\frac{2+5\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\frac{2x-4\sqrt{x}+x+3\sqrt{x}+2-2-5\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\frac{3x-6\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\frac{3\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\frac{3\sqrt{x}}{\sqrt{x}+2}\)
Ta có : \(A=\frac{3\sqrt{x}}{\sqrt{x}+2}=\frac{3\sqrt{x}+6-6}{\sqrt{x}+2}=\frac{3\left(\sqrt{x}+2\right)-6}{\sqrt{x}+2}=3-\frac{6}{\sqrt{x}+2}\)
\(A\inℤ\Leftrightarrow\frac{6}{\sqrt{x}+2}\inℤ\Leftrightarrow\sqrt{x}+2\inƯ\left(6\right)\)
đến đây bạn tự làm tiếp