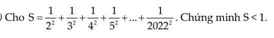Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(x - y + z) - (z - a + x) - (a - b - g)
= x - y + z - z + a - x - a + b + g
= - y + b + g
= b + g - y


Ta có: (m-Y+a)-(a-n-x)-(m+n-x)
=m-Y+a-a+n+x-m-n+x
=(m-m)+(a-a)+(n-n)+(x+x)-Y
=0+0+0+2x-Y
=2x-Y


Bài 5:
Vì \(ƯCLN\left(24,108\right)=12\) nên có thể chia nhiều nhất thành 12 tổ
Bài 6:
Vì \(BC\left(12,15,18\right)=B\left(180\right)=\left\{0;180;360;540;...\right\}\) nên khối 6 có 360 hs
Bài 6:
Gọi số học sinh là x
Theo đề, ta có: \(x\in BC\left(12;15;18\right)\)
mà 300<=x<=400
nên x=360

\(3^{n+3}+3^{n+1}+2^{n+3}+2^{n+2}=3^{n+1}\left(3^2+1\right)+2^{n+2}\left(2+1\right)=3^{n+1}.2.5+2^{n+2}.3\)
\(=2.3.\left(3^n.5+2^{n+1}\right)=6.\left(3^n.5+2^{n+1}\right)\) chia hết cho 6(đpcm)

Ta có \(\dfrac{1}{2^2}< \dfrac{1}{1.2};\dfrac{1}{3^2}< \dfrac{1}{2.3};...;\dfrac{1}{2022^2}< \dfrac{1}{2021.2022}\)
cộng vế với vế
\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{2022^2}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2021}-\dfrac{1}{2022}\)
\(=1-\dfrac{1}{2022}=\dfrac{2021}{2022}\)
Vậy ta có đpcm
 làm mỗi câu d thôi ạ
làm mỗi câu d thôi ạ
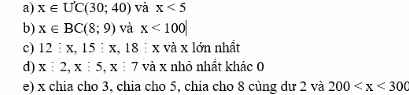 Giúp mình câu d và e thôi ạ
Giúp mình câu d và e thôi ạ