K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TQ
5
AH
Akai Haruma
Giáo viên
17 tháng 7 2021
Lời giải:
b. Tam giác $ABC$ vuông tại $A$ và $C=45^0$ nên:
$B=90^0-C=90^0-45^0=45^0$
Do đó, tam giác $ABC$ vuông cân tại $A$
$\Rightarrow AC=AB=50$ (cm)
Áp dụng định lý Pitago: $BC=\sqrt{AB^2+AC^2}=\sqrt{50^2+50^2}=50\sqrt{2}$ (cm)
f.
Theo định lý Pitago: $AC=\sqrt{BC^2-AB^2}=\sqrt{7^2-5^2}=2\sqrt{6}$ (cm)
$\sin B=\frac{AC}{BC}=\frac{2\sqrt{6}}{7}$
$\Rightarrow B=44,42^0$
$C=90^0-B=90^0-44,42^0=45,58^0$
17 tháng 7 2021
b) Xét ΔABC vuông tại A có \(\widehat{C}=45^0\)(gt)
nên ΔABC vuông cân tại A(Định nghĩa tam giác vuông cân)
Suy ra: \(\widehat{B}=45^0\) và AC=50(cm)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=50^2+50^2=5000\)
hay \(BC=50\sqrt{2}\left(cm\right)\)
A
0
18 tháng 2 2021
1) Vì x=25 thỏa mãn ĐKXĐ nên Thay x=25 vào biểu thức \(A=\dfrac{\sqrt{x}-2}{x+1}\), ta được:
\(A=\dfrac{\sqrt{25}-2}{25+1}=\dfrac{5-2}{25+1}=\dfrac{3}{26}\)
Vậy: Khi x=25 thì \(A=\dfrac{3}{26}\)
2) Ta có: \(B=\dfrac{\sqrt{x}-3}{\sqrt{x}+1}+\dfrac{2x+8\sqrt{x}-6}{x-\sqrt{x}-2}\)
\(=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-5\sqrt{x}+6+2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3x+3\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}}{\sqrt{x}-2}\)
A
, mình đang cần giải gấp. Cảm ơn mn nhiều.
1
3 tháng 9 2021
Bài 3:
a: Gọi OK là khoảng cách từ O đến AB
Suy ra: K là trung điểm của AB
hay \(AK=BK=\dfrac{AB}{2}=\dfrac{8}{2}=4\left(cm\right)\)
Áp dụng định lí Pytago vào ΔOKA vuông tại K, ta được:
\(OA^2=OK^2+KA^2\)
hay OK=3(cm)
A
1
26 tháng 9 2021
c: \(f\left(5-2\sqrt{3}\right)=f\left(2\right)\)
\(\Leftrightarrow\sqrt{4-2\sqrt{3}}+m\left(5-2\sqrt{3}\right)+2=\sqrt{2-1}+2m+2\)
\(\Leftrightarrow\sqrt{3}+1+m\left(5-2\sqrt{3}\right)=2m+3\)
\(\Leftrightarrow m\left(3-2\sqrt{3}\right)=2-\sqrt{3}\)
hay \(m=-\dfrac{\sqrt{3}}{3}\)
8 tháng 8 2021
Câu 9:
a) Ta có: \(9x^2-16=0\)
\(\Leftrightarrow\left(3x-4\right)\left(3x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{4}{3}\\x=-\dfrac{4}{3}\end{matrix}\right.\)
b) Ta có: \(4x^2=13\)
\(\Leftrightarrow x^2=\dfrac{13}{4}\)
\(\Leftrightarrow x\in\left\{\dfrac{\sqrt{13}}{2};-\dfrac{\sqrt{13}}{2}\right\}\)
c) Ta có: \(2x^2+9=0\)
\(\Leftrightarrow2x^2=-9\)(Vô lý)
d) Ta có: \(-x^2+324=0\)
\(\Leftrightarrow x^2=324\)
\(\Leftrightarrow\left[{}\begin{matrix}x=18\\x=-18\end{matrix}\right.\)
1 tháng 8 2021
39) Ta có: \(\sqrt{49-5\sqrt{96}}-\sqrt{49+5\sqrt{96}}\)
\(=\sqrt{49-20\sqrt{6}}-\sqrt{49+20\sqrt{6}}\)
\(=5-2\sqrt{6}-5-2\sqrt{6}\)
\(=-4\sqrt{6}\)
40) Ta có: \(\sqrt{35+12\sqrt{6}}-\sqrt{35-12\sqrt{6}}\)
\(=3\sqrt{3}+2\sqrt{2}-3\sqrt{3}+2\sqrt{2}\)
\(=4\sqrt{2}\)
41) Ta có: \(\sqrt{13+2\sqrt{42}}+\sqrt{13-2\sqrt{42}}\)
\(=\sqrt{7}+\sqrt{6}+\sqrt{7}-\sqrt{6}\)
\(=2\sqrt{7}\)
7 tháng 9 2021
a: Ta có: \(\left(12-6\sqrt{3}\right)\cdot\sqrt{\dfrac{3}{14-8\sqrt{3}}}-3\cdot\sqrt{2\left(1-\sqrt{1-\sqrt{4-2\sqrt{3}}}\right)+2\sqrt{4+2\sqrt{3}}}\)
\(=\left(3-\sqrt{3}\right)\cdot\dfrac{\sqrt{3}}{2\sqrt{2}-\sqrt{6}}-3\cdot\sqrt{2\cdot\left(1-\sqrt{1-\sqrt{3}+1}\right)+2\cdot\left(\sqrt{3}+1\right)}\)
\(=\left(3-\sqrt{3}\right)\cdot\dfrac{\sqrt{6}\left(2+\sqrt{3}\right)}{2}-3\cdot\sqrt{\left(2-\sqrt{2}\cdot\sqrt{4-2\sqrt{3}}\right)+2\sqrt{3}+2}\)
\(=\dfrac{\left(3\sqrt{6}-3\sqrt{2}\right)\left(2+\sqrt{3}\right)}{2}-3\cdot\sqrt{2-\sqrt{2}\left(\sqrt{3}+1\right)+2\sqrt{3}+2}\)
\(=\dfrac{3\sqrt{6}+3\sqrt{2}}{2}-3\cdot\sqrt{2-\sqrt{6}-\sqrt{2}+2\sqrt{3}+2}\)
Đến đây thì xin lỗi bạn, mình thua
7 tháng 9 2021
b: Ta có: \(x^4+6x^3+11x^2+6x+1\)
\(=x^4+3x^3+x^2+3x^3+9x^2+3x+x^2+3x+1\)
\(=\left(x^2+3x+1\right)^2\) là số chính phương(đpcm)
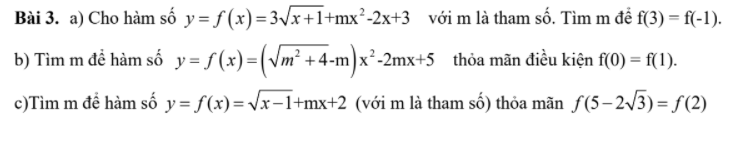
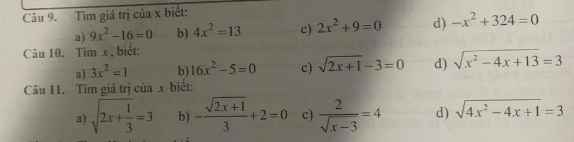
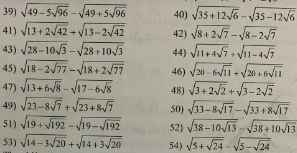
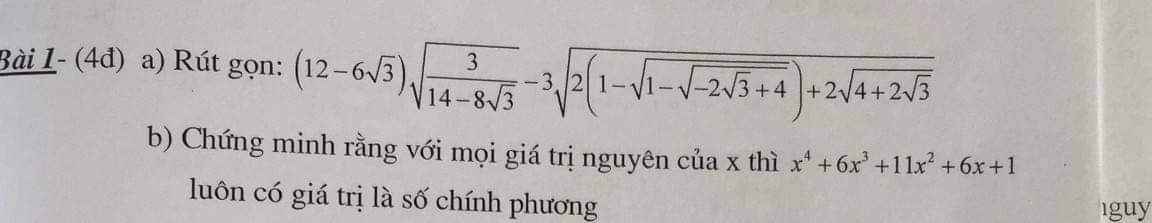
Câu 15:
1: Ta có: \(\sqrt{2x+5}=\sqrt{1-x}\)
\(\Leftrightarrow2x+5=1-x\)
\(\Leftrightarrow2x+x=1-5\)
\(\Leftrightarrow3x=-4\)
hay \(x=-\dfrac{4}{3}\)
2: Ta có: \(\sqrt{2x-1}=\sqrt{x-1}\)
\(\Leftrightarrow2x-1=x-1\)
\(\Leftrightarrow x=0\)(loại
3: Ta có: \(\sqrt{x^2-x}=\sqrt{3x-5}\)
\(\Leftrightarrow x^2-x=3x-5\)
\(\Leftrightarrow x^2-4x+5=0\)
\(\Leftrightarrow\left(x-2\right)^2+1=0\)(vô lý
4: Ta có: \(\sqrt{2x^2-3}=\sqrt{4x-3}\)
\(\Leftrightarrow2x^2=4x\)
\(\Leftrightarrow2x^2-4x=0\)
\(\Leftrightarrow2x\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=2\left(nhận\right)\end{matrix}\right.\)
5: Ta có: \(\sqrt{x^2-x}=\sqrt{3-x}\)
\(\Leftrightarrow x^2=3\)
\(\Leftrightarrow x\in\left\{\sqrt{3};-\sqrt{3}\right\}\)