Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
sin ( - 50 ο ) < 0 ; tan 170 ο < 0 ;
cos ( - 90 ο ) < 0 ; sin 530 ο > 0 ,
do đó tích của chúng âm
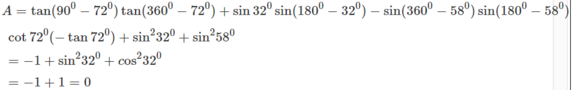
a)\(sin^2\left(180^o-\alpha\right)+tan^2\left(180-\alpha\right).tan^2\left(270^o+\alpha\right)\)\(+sin\left(90^o+\alpha\right)cos\left(\alpha-360^o\right)\)
\(=sin^2\alpha+tan^2\alpha.cot^2\alpha+cos\alpha cos\alpha\)
\(=sin^2\alpha+cos^2\alpha+\left(tan\alpha cot\alpha\right)^2=1+1=2\).
\(\dfrac{cos\left(\alpha-180^o\right)}{sin\left(180^o-\alpha\right)}+\dfrac{tan\left(\alpha-180^o\right)cos\left(180^o+\alpha\right)sin\left(270^o+\alpha\right)}{tan\left(270^o+\alpha\right)}\)
\(=\dfrac{cos\left(180^o-\alpha\right)}{sin\left(180^o-\alpha\right)}+\dfrac{-tan\left(180^o-\alpha\right).cos\alpha.sin\left(90^o+\alpha\right)}{-tan\left(90^o+\alpha\right)}\)
\(=tan\left(180^o-\alpha\right)+\dfrac{tan\alpha.cos\alpha.cos\alpha}{cot\alpha}\)
\(=-tan\alpha+tan^2\alpha cos^2\alpha\)
\(=tan\alpha\left(-1+tan\alpha cos^2\alpha\right)\)
\(=tan\alpha\left(sin\alpha cos\alpha-1\right)\).
a)
Đặt \(A = \left( {2\sin {{30}^o} + \cos {{135}^o} - 3\tan {{150}^o}} \right).\left( {\cos {{180}^o} - \cot {{60}^o}} \right)\)
Ta có: \(\left\{ \begin{array}{l}\cos {135^o} = - \cos {45^o};\cos {180^o} = - \cos {0^o}\\\tan {150^o} = - \tan {30^o}\end{array} \right.\)
\( \Rightarrow A = \left( {2\sin {{30}^o} - \cos {{45}^o} + 3\tan {{30}^o}} \right).\left( { - \cos {0^o} - \cot {{60}^o}} \right)\)
Sử dụng bảng giá trị lượng giác của một số góc đặc biệt, ta có:
\(\left\{ \begin{array}{l}\sin {30^o} = \frac{1}{2};\tan {30^o} = \frac{{\sqrt 3 }}{3}\\\cos {45^o} = \frac{{\sqrt 2 }}{2};\cos {0^o} = 1;\cot {60^o} = \frac{{\sqrt 3 }}{3}\end{array} \right.\)
\( \Rightarrow A = \left( {2.\frac{1}{2} - \frac{{\sqrt 2 }}{2} + 3.\frac{{\sqrt 3 }}{3}} \right).\left( { - 1 - \frac{{\sqrt 3 }}{3}} \right)\)
\(\begin{array}{l} \Leftrightarrow A = - \left( {1 - \frac{{\sqrt 2 }}{2} + \sqrt 3 } \right).\left( {1 + \frac{{\sqrt 3 }}{3}} \right)\\ \Leftrightarrow A = - \frac{{2 - \sqrt 2 + 2\sqrt 3 }}{2}.\frac{{3 + \sqrt 3 }}{3}\\ \Leftrightarrow A = - \frac{{\left( {2 - \sqrt 2 + 2\sqrt 3 } \right)\left( {3 + \sqrt 3 } \right)}}{6}\\ \Leftrightarrow A = - \frac{{6 + 2\sqrt 3 - 3\sqrt 2 - \sqrt 6 + 6\sqrt 3 + 6}}{6}\\ \Leftrightarrow A = - \frac{{12 + 8\sqrt 3 - 3\sqrt 2 - \sqrt 6 }}{6}.\end{array}\)
b)
Đặt \(B = {\sin ^2}{90^o} + {\cos ^2}{120^o} + {\cos ^2}{0^o} - {\tan ^2}60 + {\cot ^2}{135^o}\)
Ta có: \(\left\{ \begin{array}{l}\cos {120^o} = - \cos {60^o}\\\cot {135^o} = - \cot {45^o}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{\cos ^2}{120^o} = {\cos ^2}{60^o}\\{\cot ^2}{135^o} = {\cot ^2}{45^o}\end{array} \right.\)
\( \Rightarrow B = {\sin ^2}{90^o} + {\cos ^2}{60^o} + {\cos ^2}{0^o} - {\tan ^2}60 + {\cot ^2}{45^o}\)
Sử dụng bảng giá trị lượng giác của một số góc đặc biệt, ta có:
\(\left\{ \begin{array}{l}\cos {0^o} = 1;\;\;\cot {45^o} = 1;\;\;\cos {60^o} = \frac{1}{2}\\\tan {60^o} = \sqrt 3 ;\;\;\sin {90^o} = 1\end{array} \right.\)
\( \Rightarrow B = {1^2} + {\left( {\frac{1}{2}} \right)^2} + {1^2} - {\left( {\sqrt 3 } \right)^2} + {1^2}\)
\( \Leftrightarrow B = 1 + \frac{1}{4} + 1 - 3 + 1 = \frac{1}{4}.\)
c
Đặt \(C = \cos {60^o}.\sin {30^o} + {\cos ^2}{30^o}\)
Sử dụng bảng giá trị lượng giác của một số góc đặc biệt, ta có:
\(\sin {30^o} = \frac{1}{2};\;\;\cos {30^o} = \frac{{\sqrt 3 }}{2};\;\cos {60^o} = \frac{1}{2}\;\)
\( \Rightarrow C = \frac{1}{2}.\frac{1}{2} + {\left( {\;\frac{{\sqrt 3 }}{2}} \right)^2} = \frac{1}{4} + \frac{3}{4} = 1.\)
Ta có: \(\sin {70^o} = \cos {20^o};\;\cos {110^o} = - \cos {70^o} = - \sin {20^o}\)
\(\begin{array}{l} \Rightarrow A = {(\sin {20^o} + \cos {20^o})^2} + {(\cos {20^o} - \sin {20^o})^2}\\ = ({\sin ^2}{20^o} + {\cos ^2}{20^o} + 2\sin {20^o}\cos {20^o}) + ({\cos ^2}{20^o} + {\sin ^2}{20^o} - 2\sin {20^o}\cos {20^o})\\ = 2({\sin ^2}{20^o} + {\cos ^2}{20^o})\\ = 2\end{array}\)
Ta có: \(\tan {110^o} = - \tan {70^o} = - \cot {20^o};\;\cot {110^o} = - \cot {70^o} = - \tan {20^o}.\)
\( \Rightarrow B = \tan {20^o} + \cot {20^o} + ( - \cot {20^o}) + ( - \tan {20^o}) = 0\)
\(A=tan18^otan288+sin32^osin148^o-sin302^osin122^o\)
\(=tan18^o.tan\left(-72^o\right)+sin32^o.sin32^o+sin58^o.sin58^o\)
\(=-tan18^o.cot18^o+sin^232^o+sin^258^o\)
\(=-1+sin^232^o+cos^232^2=-1+1=0\).
b) \(B=\dfrac{1+sin^4\alpha-cos^4\alpha}{1-sin^6\alpha-cos^6\alpha}\)
\(=\dfrac{1+\left(sin^2\alpha+cos^2\alpha\right)\left(sin^2\alpha-cos^2\alpha\right)}{1-\left(sin^6\alpha+cos^6\alpha\right)}\)
\(=\dfrac{1+sin^2\alpha-cos^2\alpha}{1-\left(sin^2\alpha+cos^2\alpha\right)\left(sin^2\alpha-sin\alpha cos\alpha+cos^2\alpha\right)}\)
\(=\dfrac{sin^2\alpha+1-cos^2\alpha}{1-\left(1-sin\alpha.cos\alpha\right)}\)
\(=\dfrac{sin^2\alpha+sin^2\alpha}{sin\alpha cos\alpha}\)
\(=\dfrac{2sin^2\alpha}{sin\alpha cos\alpha}=\dfrac{2sin\alpha}{cos\alpha}=2tan\alpha\).
Bạn kiểm tra lại đề bài câu 1, câu này chỉ có thể rút gọn đến \(2cot^2x+2cotx+1\) nên biểu thức ko hợp lý
Đồng thời kiểm tra luôn đề câu 2, trong cả 2 căn thức đều xuất hiện \(6sin^2x\) rất không hợp lý, chắc chắn phải có 1 cái là \(6cos^2x\)
a) \(A = \cos {0^o} + \cos {40^o} + \cos {120^o} + \cos {140^o}\)
Tra bảng giá trị lượng giác của một số góc đặc biệt, ta có:
\(\cos {0^o} = 1;\;\cos {120^o} = - \frac{1}{2}\)
Lại có: \(\cos {140^o} = - \cos \left( {{{180}^o} - {{40}^o}} \right) = - \cos {40^o}\)
\(\begin{array}{l} \Rightarrow A = 1 + \cos {40^o} + \left( { - \frac{1}{2}} \right) - \cos {40^o}\\ \Leftrightarrow A = \frac{1}{2}.\end{array}\)
b) \(B = \sin {5^o} + \sin {150^o} - \sin {175^o} + \sin {180^o}\)
Tra bảng giá trị lượng giác của một số góc đặc biệt, ta có:
\(\sin {150^o} = \frac{1}{2};\;\sin {180^o} = 0\)
Lại có: \(\sin {175^o} = \sin \left( {{{180}^o} - {{175}^o}} \right) = \sin {5^o}\)
\(\begin{array}{l} \Rightarrow B = \sin {5^o} + \frac{1}{2} - \sin {5^o} + 0\\ \Leftrightarrow B = \frac{1}{2}.\end{array}\)
c) \(C = \cos {15^o} + \cos {35^o} - \sin {75^o} - \sin {55^o}\)
Ta có: \(\sin {75^o} = \cos\left( {{{90}^o} - {{75}^o}} \right) = \cos {15^o}\); \(\sin {55^o} = \cos\left( {{{90}^o} - {{55}^o}} \right) = \cos {35^o}\)
\(\begin{array}{l} \Rightarrow C = \cos {15^o} + \cos {35^o} - \cos {15^o} - \cos {35^o}\\ \Leftrightarrow C = 0.\end{array}\)
d) \(D = \tan {25^o}.\tan {45^o}.\tan {115^o}\)
Ta có: \(\tan {115^o} = - \tan \left( {{{180}^o} - {{115}^o}} \right) = - \tan {65^o}\)
Mà: \(\tan {65^o} = \cot \left( {{{90}^o} - {{65}^o}} \right) = \cot {25^o}\)
\(\begin{array}{l} \Rightarrow D = \tan {25^o}.\tan {45^o}.(-\cot {25^o})\\ \Leftrightarrow D =- \tan {45^o} = -1\end{array}\)
e) \(E = \cot {10^o}.\cot {30^o}.\cot {100^o}\)
Ta có: \(\cot {100^o} = - \cot \left( {{{180}^o} - {{100}^o}} \right) = - \cot {80^o}\)
Mà: \(\cot {80^o} = \tan \left( {{{90}^o} - {{80}^o}} \right) = \tan {10^o}\Rightarrow \cot {100^o} =- \tan {10^o}\)
\(\begin{array}{l} \Rightarrow E = \cot {10^o}.\cot {30^o}.(-\tan {10^o})\\ \Leftrightarrow E = -\cot {30^o} =- \sqrt 3 .\end{array}\)
