Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

sin 1280 ο = sin ( 3 . 360 ο + 120 ο ) = sin 200 ο < 0
cos 1280 ο = cos 200 ο < 0

sin ( - 1876 ο ) = sin ( - 1800 ο - 76 ο ) = sin ( - 76 ο ) = - sin 76 ο < 0
cos ( - 1876 ο ) = cos ( - 76 ) ο = cos 76 ο > 0

sin ( - 235 ο ) = sin ( - 180 ο - 55 ο ) = - sin ( - 55 ο ) = sin 55 ο > 0 , cos ( - 235 ο ) < 0

a) Do \(90^o< \alpha< 180^o\) nên \(sin\alpha>0;cos\alpha< 0\).
b) Do \(180^o< \alpha< 270^o\) nên \(sin\alpha< 0;cos\alpha< 0\).
c) Do \(270^o< \alpha< 360^o\) nên \(sin\alpha< 0;cos\alpha>0\).
d) \(\alpha=1280^o=3.360^o+200^o\)
\(sin1280^o=sin\left(3.360^o+200^o\right)=sin200^o< 0\).
e)
\(sin\left(-235^o\right)=sin\left(-235^o+360^o\right)=sin125^o>0\).
\(cos\left(-235^o\right)=cos\left(-235^o+360^o\right)=cos125^o< 0\).
d) \(sin\left(-1876\right)=sin\left(-1876^o+1800^o\right)=sin\left(-76^o\right)\)\(=-sin76^o< 0\).
\(cos\left(-1876^o\right)=cos\left(-76^o\right)=cos76^o>0\).

a) \(sin110^ocos130^otan30^ocot320^o\)
Ta có \(sin110^o>0;cos130^o< 0;tan30^o>0;cot320^o< 0\) nên
\(sin110^ocos130^otan30^ocot320^o>0\).
b) \(sin\left(-50^o\right)tan170^ocos\left(-91^o\right)sin530^o\)
\(=-sin50^otan170^o.cos91^osin170^o\)
Do \(sin50^o>0;tan170^o< 0;cos91^o< 0,sin170^o>0\)
nên \(=-sin50^otan170^o.cos91^osin170^o< 0\)
hay \(sin\left(-50^o\right)tan170^ocos\left(-91^o\right)sin530^o< 0\).
a) Ta có :
\(\sin110^0>0;\cos130^0< 0;\tan30^0>0;cot320^0< 0\)
do đó tích của chúng dương.
b) \(\sin\left(-50^0\right)< 0;tan170^0< 0;\cos\left(-91^0\right)< 0;\sin530^0>0\)
do đó tích của chúng âm.

+) Định nghĩa của sin α; cos α
Trên đường tròn lượng giác, xét cung AM có số đo α
Gọi H và K lần lượt là hình chiếu của M trên trục Ox, Oy.
Tung độ y = OK¯ của điểm M được gọi là sin của α : sin α = OK¯
Hoành độ x = OH¯ của điểm M được gọi là cos của α : cos α = OH¯
Trên đường tròn lượng giác trong mặt phẳng Oxy, lấy điểm A (1; 0) làm gốc.
Khi đó các cung có số đo hơn kém nhau một bội của 2π có điểm cuối trùng nhau.
Giả sử cung α có điểm cuối là M(x; y)
Khi đó với mọi k ∈ Z thì cung α + k2π cũng có điểm cuối là M.
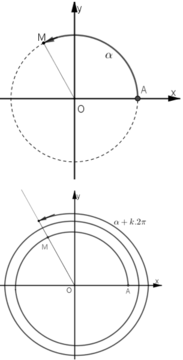
sin α = y, sin (α + k2π) = y nên sin(α + k2π) = sinα
cos α = x, cos(α + k2π) = x nên cos(α + k2π) = cosα
sin 135 o > 0, cos 135 o < 0