Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi x (Km/ h)là vận tốc của ca nô khi nước yên lặng
vận tốc khi đi suôi dòng là x + 3
vận tốc khi đi ngực dòng là x - 3
thời gian khi đi suôi dòng là \(\dfrac{30}{x+3}\)
thời gian khi đi ngực dòng là \(\dfrac{30}{x-3}\)
thời gian nghỉ là 40 phút = \(\dfrac{40}{60}\) = \(\dfrac{2}{3}\) giờ
vì tổng thời gian từ lúc đi đến lúc trở về là 6 giờ
nên ta có phương trình :
\(\dfrac{30}{x+3}\)+\(\dfrac{30}{x-3}\)+\(\dfrac{2}{3}\) = 6
\(\Leftrightarrow\) \(\dfrac{30.\left(x-3\right)+30.\left(x+3\right)}{\left(x+3\right)\left(x-3\right)}\) +\(\dfrac{2}{3}\) = 6
\(\Leftrightarrow\) \(\dfrac{60x}{x^2-9}\)+\(\dfrac{2}{3}\) = 6\(\Leftrightarrow\) \(\dfrac{60x}{x^2-9}\)= \(\dfrac{16}{3}\)
\(\Leftrightarrow\) 180x = 16x2 - 144\(\Leftrightarrow\) 16x2 -180x -144 = 0
\(\Leftrightarrow\) 4x2 - 45x -36 = 0
giải \(\Delta\) ta có 2 nghiệm :x1=12 (tmđk) ; x2=-\(\dfrac{3}{4}\) (loại)
vậy vận tốc khi nước yên lặng là 12(Km/h)

Gọi x (km/h) là vận tốc của ca nô khi nước yên lặng.
Điều kiện: x > 3
Khi đó vận tốc khi đi xuôi dòng trên sông là x + 3 (km/h)
vận tốc khi đi ngược dòng trên sông là x – 3 (km/h)
thời gian ca nô đi xuôi dòng là 30/(x + 3) (giờ)
thời gian ca nô đi ngược dòng là 30/(x - 3) (giờ)
thời gian ca nô nghỉ ở B là 40 phút = 2/3 (giờ)
Theo đề bài, ta có phương trình:
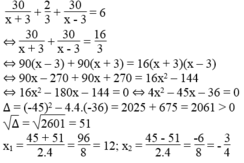
Giá trị x = - 3/4 không thỏa mãn điều kiện bài toán.
Vậy vận tốc của ca nô khi nước yên lặng là 12 km/h.

Gọi vận tốc thực của canô là x (km/h) (x > 3)
Gọi vận tốc xuôi dòng là : x + 3 (km/h)
Gọi vận tốc khi ngược dòng là : x – 3 (km/h)

Do kể từ lúc khởi hành đến khi về tới bến A hết tất cả 6 h nên ta có:
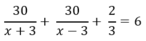
⇔ 30.3 (x- 3) + 30.3. (x+ 3) + 2(x+ 3). (x – 3) = 6.3.(x+3).(x – 3)
⇔ 90.(x – 3) + 90(x+ 3)+ 2(x2 – 9) = 18 (x2 -9)
⇔ 90x – 270+ 90x + 270 + 2x2 – 18 = 18x2 – 162
⇔ 180x + 2x2 – 18 = 18x2 – 162
⇔ 16x2 – 180x -144= 0
⇔ 4x2 –45x – 36 = 0
Có a=4; b= - 45, c= - 36
∆= ( -45)2 – 4.4.(- 36)= 2601 > 0
Phương trình đã cho có hai nghiệm là:
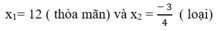
Vậy vận tốc của canô trong nước yên lặng là 12km/h.

Gọi vận tốc thực của canô là x (km/h) (x > 3)
Gọi vận tốc xuôi dòng là : x + 3 (km/h)
Gọi vận tốc khi ngược dòng là : x – 3 (km/h)

Do kể từ lúc khởi hành đến khi về tới bến A hết tất cả 6 h nên ta có:
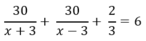
⇔ 30.3 (x- 3) + 30.3. (x+ 3) + 2(x+ 3). (x – 3) = 6.3.(x+3).(x – 3)
⇔ 90. ( x − 3 ) + 90 ( x + 3 ) + 2 x 2 − 9 = 18 x 2 − 9 ⇔ 90 x − 270 + 90 x + 270 + 2 x 2 − 18 = 18 x 2 − 162 ⇔ 180 x + 2 x 2 − 18 = 18 x 2 − 162 ⇔ 16 x 2 − 180 x − 144 = 0 ⇔ 4 x 2 − 45 x − 36 = 0
Có a=4; b= - 45, c= - 36
∆ = ( - 45 ) 2 – 4 . 4 . ( - 36 ) = 2601 > 0
Phương trình đã cho có hai nghiệm là:
![]()
Vậy vận tốc của canô trong nước yên lặng là 12km/h.

gọi vận tốc dòng nước là x
theo bài ra ta có
thời gian lúc đi xuôi = \(\frac{48}{28+x}\)
thời gian lúc đi ngược \(=\frac{48}{28-x}\)
vì thời lúc về lâu hơn thời gian lúc đi 30'
=> \(\frac{48}{28+x}=\frac{48}{28-x}-\frac{1}{2}\)
giải ra là xong nha
_Kudo_

bài này hệ là \(\frac{30}{x-3}+\frac{30}{x+3}=6-\frac{40}{60}\)