Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn:
Gọi thời gian phải tìm là x (Phút)
Gọi thời gian Khiêm đi từ nhà đến trường là a (Phút)
Số xe Khiêm gặp khi đi từ nhà đến trường đi theo hướng ngược lại là: a/10
Số xe Khiêm gặp khi đi từ nhà đến trường đi theo hướng cùng chiều là: a/x
Số xe đi qua Khiêm khi Khiêm đi từ nhà đến trường cũng chính là số xe đã đi trên đoạn đường từ nhà Khiêm đến trường theo cả 2 chiều là: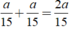
Ta có phương trình: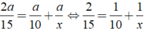
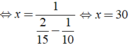
Vậy cứ sau 30 phút lại có xe cùng chiều vượt qua Khiêm.

Đáp án D
Gọi thời gian phải tìm là x (Phút)
Gọi thời gian Khiêm đi từ nhà đến trường là a (Phút)
Số xe Khiêm gặp khi đi từ nhà đến trường đi theo hướng ngược lại là: a/10
Số xe Khiêm gặp khi đi từ nhà đến trường đi theo hướng cùng chiều là: a/x
Số xe đi qua Khiêm khi Khiêm đi từ nhà đến trường cũng chính là số xe đã đi trên đoạn đường từ nhà Khiêm đến trường theo cả 2 chiều là: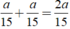
Ta có phương trình: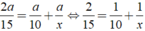
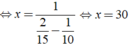
Vậy cứ sau 30 phút lại có xe cùng chiều vượt qua Khiêm.

Gọi x (phút ) là thời gian người khách dó đi từ A đến B
suy ra :Trong x phút người đo gắp x/15 chuyến xe buýt đi từ A đến Bđồng thời gắp x/10 chuyến xe buýt đi từ B tới A
Nếu khi đến B, người đó quay về A ngay thì trong x phút ,người đó gắp x/15 chuyến đi từ B về A đồng thời x/10 phút đi từ A về B
suy ra trong vòng 2x (phút) người đó gặp :x/15+x/10=x/5 (chuyến ) xe buýt đi từ A về B
Thời gian cấc xe lần lượt rời bến là : 2x:x/6=12 phút

Gọi x (phút ) là thời gian người khách đó đi từ A đến B
=> Trong x phút, người đó gặp \(\frac{x}{15}\) chuyến xe buýt đi từ A tới B đồng thời gặp \(\frac{x}{10}\) chuyến xe buýt đi từ B tới A
Nếu khi đến B, người đó quay về A ngay thì trong x phút: người đó gặp \(\frac{x}{15}\) chuyến đi từ B về A đồng thời \(\frac{x}{10}\) phút đi từ A về B
=> Trong vòng 2x (phút) người đó gặp : \(\frac{x}{15}\) + \(\frac{x}{10}\) = \(\frac{x}{6}\) (chuyến ) xe buýt đi từ A về B
=> Thời gian các xe lần lượt rời bến là sau: 2x : \(\frac{x}{6}\) = 12 phút
Gọi quãng đường nằm ngang là x
=> Thời gian đi trên đoạn nằm ngang đi về là 2x/15
=> Thời gian xuống dốc là 2(30 -x)/20 (xuống dốc lúc đi DB, xuống dốc lúc về AC, công lại chính là tổng đoạn đường trừ đi đường ngang)
=> Thời gian lên dốc là 2(30 -x)/10
*̀ 4h25 =4 + 5/12 = 53/12
Ta có phương trình
2[x/15 + (30 -x)/20 + (30-x)/10] = 53/12
Giải ra x

Gọi thời gian phải tìm là x (phút)
Gọi thời gian Khiêm đi từ nhà đến trường là a (phút)
Số xe Khiêm gặp khi đi từ nhà đến trường đi theo hướng ngược lại là: \(\frac{a}{10}\)
Số xe Khiêm gặp khi đi từ nhà đến trường đi theo hướng cùng chiều là: \(\frac{a}{x}\)
Số xe đi qua Khiêm khi Khiêm đi từ nhà đến trường cũng chính là số xe đã đi trên đoạn đường từ nhà Khiêm đến trường theo cả 2 chiều là: \(\frac{a}{15}+\frac{a}{15}=\frac{2a}{15}\)
Ta có phương trình: \(\frac{2a}{15}=\frac{a}{10}+\frac{a}{x}\Leftrightarrow\frac{2}{15}=\frac{1}{10}+\frac{1}{x}\Leftrightarrow x=\frac{1}{\frac{2}{15}-\frac{1}{10}}\Leftrightarrow x=30\)
Vậy cứ sau 30 phút lại có xe cùng chiều vượt qua Khiêm
Gọi thời gian phải tìm là x (Phút)
Gọi thời gian Khiêm đi từ nhà đến trường là a (Phút)
Số xe Khiêm gặp khi đi từ nhà đến trường đi theo hướng ngược lại là: a/10
Số xe Khiêm gặp khi đi từ nhà đến trường đi theo hướng cùng chiều là: a/x
Số xe đi qua Khiêm khi Khiêm đi từ nhà đến trường cũng chính là số xe đã đi trên đoạn đường từ nhà Khiêm đến trường theo cả 2 chiều là: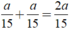
Ta có phương trình: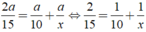
Vậy cứ sau 30 phút lại có xe cùng chiều vượt qua Khiêm.
Chọn đáp án C.