Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hàm \(y=f\left(x\right)\) có đồ thị (C):
\(\Rightarrow\) Khi tịnh tiến lên a đơn vị ta sẽ được đồ thị hàm \(y=f\left(x\right)+a\)
Khi tịnh tiến xuống dưới a đơn vị ta được đồ thị hàm \(y=f\left(x\right)-a\)
- Khi tịnh tiến sang phải a đơn vị ta sẽ được đồ thị hàm \(y=f\left(x-a\right)\)
- Khi tịnh tiến sang trái a đơn vị sẽ được đồ thị hàm \(y=f\left(x+a\right)\)
Do đó:
Khi tịnh tiến (P) lên 4 đơn vị ta được đồ thị hàm \(y=4x^2+4\)
Khi tịnh tiến (P) sang phải 2 đơn vị ta được đồ thị hàm: \(y=4\left(x-2\right)^2=4x^2-16x+16\)

Theo quy tắc dịch đồ thị ta sẽ được hàm \(y=-\left(x+2\right)^2+2-\frac{1}{2}\)
Bạn tự rút gọn

a: Thay x=3 và y=0 vào (1), ta được:
\(6-3m=0\)
hay m=2
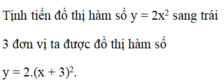




Khi tịnh tiến đồ thị \(y=f\left(x\right)\) sang trái m đơn vị ta được đồ thị hàm \(y=f\left(x+m\right)\)
Cụ thể trong bài này được đồ thị hàm \(y=2\left(x+2\right)^2\)