Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sau khoảng thời gian \(\tau\) thì số hạt nhân còn lại là
\(N = N_0 2^{-\frac{\tau}{T}}\)
=> \(\frac{N}{N_0}= \frac{1}{4}= 2^{-2}= 2^{-\frac{\tau}{T}}\)
=> \(\tau = 2T.\)
Sau khoảng thời gian \(2\tau\) thì số hạt còn lại là
\(N_1 = N_02^{-\frac{2\tau}{T}}= N_0.2^{-\frac{4T}{T}}= \frac{1}{16}N_0\)
=> Số hạt còn lại chiếm 6,25 % số hạt ban đầu.

Năng lượng tỏa ra : \(W_{tỏa} = K_{sau}-K_{trước}= K_C + K_D - K_A = -0,81 MeV\)
\(K_{tỏa}<0\) nên phản ứng là thu năng lượng
=> Khối lượng của hệ hạt giảm : \(\Delta m = \frac{W_{tỏa}}{c^{2}}=1,44.10^{-30}kg=1,44.10^{-27}g\)
Chọn C.

Cứ mỗi hạt nhân Pôlôni bị phân rã tạo thành 1 hạt nhân chì trong mẫu.
Số hạt nhân Pôlôni bị phân rã là \(\Delta N = N_0 2^{-\frac{t}{T}}.\)
Số hạt nhân Pônôni còn lại là \( N = N_0 2^{-\frac{t}{T}}.\)
Tại thời điểm t1 : \(\frac{\Delta N}{N } = \frac{1-2^{-\frac{t_1}{T}}}{2^{-\frac{t_1}{T}}}= \frac{1}{3}\)
=> \(3(1-2^{-\frac{t_1}{T}})= 2^{-\frac{t_1}{T}}\)
=> \(2^{-\frac{t_1}{T}}= 2^{-2}\)
=> \(t_1 = 2T\)
=> \(t_2 = 2T+276 = 552 \) (ngày)
=> \(\frac{t_2}{T}= \frac{552}{138}= 4.\)
Tại thời điểm t2 : \(\frac{\Delta N_1}{N_1 } = \frac{1-2^{-\frac{t_2}{T}}}{2^{-\frac{t_2}{T}}}= \frac{1-2^{-4}}{2^{-4}}= 15.\)
=> \(\frac{N_1}{\Delta N_1} = \frac{1}{15}.\)

Số hạt nhân chưa phóng xạ chính là số hạt nhân còn lại
\(N= N_0 2^{-\frac{t}{T}}= N_0 .2^{-4}= \frac{1}{16}N_0.\)
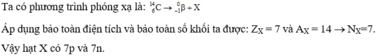
Chọn A