Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
- Đổi: 45 phút = 0,75 giờ
- Vận tốc trung bình của người đó trên quãng đường là:
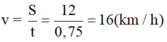

a)ta có:
vận tốc người đó là:
90/(9-7)=45km/h
b)ta có:
thời gian người đó đi 30km là:
30/45=2/3h
thời gian người đó còn lại là:
2-2/3-0.5=5/6h
vận tốc người đó phải đi để kịp giờ là:
(90-30)/(5/6)=72km/h
a) Vận tốc của người đi xe máy là
V= S /t= 90/(9-7)=45(Km/h)
b) Thời gian người đi xe máy
t= S/ V= 30/ 45=2/3 (h)
Vận tốc người đi xe máy đi để lịp thời gian dự định ban đầu
V=S /t=(90-30)/(2-2/3-0,5)=72(Km/h)

14/2 thời gian đã đi là 1/2 thời gian dự định hay 1/2 thời gian đi 1/3 đoạn đường đầu?

Thời gian dự định đi quãng đường trên :
\(t=s:v=60:30=2\left(h\right)\)
Thời gian đi \(\dfrac{1}{4}\) quãng đường :
\(t_1=\dfrac{s}{4v}=\dfrac{60}{30.4}=\dfrac{1}{2}\left(h\right)\)
Thời gian đi quãng còn lại để về sớm hơn 30 ' là :
\(t_2=2-\left(\dfrac{1}{2}+\dfrac{1}{2}\right)=1\left(h\right)\)
Vận tốc phải đi quãng đường còn lại :
\(v_2=\dfrac{s_2}{t_2}=\dfrac{3.60}{4.1}=45\left(\dfrac{km}{h}\right)\)
Thời gian dự định:
\(t=\dfrac{S}{v}=\dfrac{60}{30}=2h\)
Thời gian người đó đi hết \(\dfrac{1}{2}\) quãng đường đầu:
\(t=\dfrac{S'}{v}=\dfrac{\dfrac{1}{2}S}{v}=\dfrac{\dfrac{1}{2}\cdot60}{30}=1h\)
Thời ian còn lại để đến sớm hơn 30 phút:
\(t'=2-1-\dfrac{30}{60}=0,5h=30'\)
Vận tốc người đó phải đi:
\(v'=\dfrac{S'}{t'}=\dfrac{S-\dfrac{1}{2}S}{t'}=\dfrac{60-\dfrac{1}{2}\cdot60}{0,5}=60\)km/h

Bài 1:
a)Thời gian xe thứ nhất chạy xong quãng đường là:\(t=\frac{s}{v_1}=\frac{60}{30}=2\left(h\right)\)
Giả sử sau 1 giờ, xe thứ hai chạy đến M
Thời gian xe thứ hai chạy từ M đến hết quãng đường kể cả nghỉ là:
t* = 2 + 0,5 = 2,5 (h)
Thời gian thực để xe hai đi hết quãng đường là:
t** = t* + 1 − 0,75 = 2,5 + 1 − 0,75 = 2,75 (h)
Vận tốc xe hai là:
v = s/t** = 60/2,75 = 21, (81) (km/h)
b)Để xe 2 đến nơi cùng lúc với xe 1 thì t* = 2
=> t** = t* + 1 - 0,75 = 2 + 1 - 0,75 = 2,25
=> v = s/t** = 60/2,25 = 26, (6) (km/h)
a)
Sau 2h thì người đi xe đạp đi được:
S1 = 12 . 2 = 24(km)
Vậy ta có thể coi 2 người bắt đầu đi từ lúc 8h, và khoảng cách giữa 2 người là
S = AB − S1 = 48 - 24 = 24 (km)
=> Kể từ lúc 8h thì thời gian để 2 người gặp nhau là:
\(t=\frac{S_1}{12+4}=1,5\left(h\right)\)
Vậy 2 người gặp nhau lúc 9h30' và cách A:
S=S1+12. 1,5 = 42 (km)
b)
Ta có: Thời gian người đi xe đạp đi trước người đi bộ là 2h nhưng người đi xe đạp lại nghỉ 1h nên ta coi người đi xe đạp đi trước người đi bộ 1h.
Sau 1h thì người đi xe đạp đi được:
S1 = 12 . 1 =12(km)
Vậy ta có thể coi 2 người bắt đầu đi từ lúc 8h, và khoảng cách giữa 2 người là
S = AB − S1 = 36km
=> Kể từ lúc 8h thì thời gian để 2 người gặp nhau là:
\(t=\frac{S_1}{12+4}=2,25\left(h\right)\)
Vậy 2 người gặp nhau lúc 10h15' và cách A:
S = S1 + 12 . 2,25 = 39km

30'=0,5h
ta có:
thời gian người đó đi 1/4 quãng đường đầu là:
\(t_1=\frac{S_1}{v_1}=\frac{S}{4v_1}=\frac{80}{160}=0,5h\)
thời gian người đó đi hết quãng đường còn lại là:
\(t_2=\frac{S_2}{v_2}=\frac{3S}{4v_2}=\frac{320}{4v_2}\)
thời gian dự định của người đó là:
\(t=\frac{S}{v}=2h\)
do người ấy tới sơm hơn 30' so với dự định nên:
\(0,5+\frac{320}{4v_2}=2-0,5\)
\(\Rightarrow v_2=80\) km/h

Vận tốc người đi xe đạp đi nửa quãng đường còn lại là:
\(v_{tb}=\dfrac{2}{\dfrac{1}{12}+\dfrac{1}{v_2}}=\dfrac{2}{\dfrac{1}{4}}=8\left(\dfrac{km}{h}\right)\)
=> \(\dfrac{1}{4}-\dfrac{1}{12}=\dfrac{1}{6}\) => \(v_2=6\left(\dfrac{km}{h}\right)\)
Đáp số: 6 km/h.
Vtb = (S1 + S2)/(t1 + t2)=2S1/(S1/V1 + S2/V2) = 2/(1/V1 + 1/V2) ( cùng rút gọn cho S1)
<=> 8 = 2/(1/12 + 1/V2) => V2 = 6 (km/h)
Vậy vận tốc trên quãng đường còn lại là 6km/h.