Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B
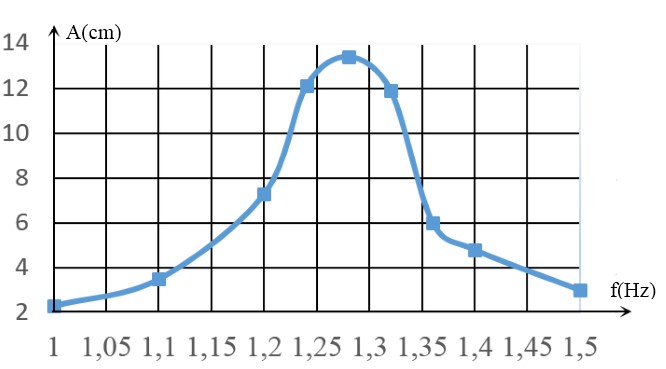
Dựa vào đồ thị ra nhận thấy vị trí A lớn nhất là tại f xấp xỉ bằng 1,28 Hz.
Suy ra tại f = 1,28 Hz xảy ra hiện tượng cộng hưởng
=> Tần số riêng của hệ: f 0 = 1,28 Hz.
⇒ f 0 = 1 2 π k m
⇒ k = m . f 0 2 .4 π 2
= 0 , 216.1 , 28 2 .4 π 2 = 13 , 97 N / m .

Đáp án A
Ta thấy con lắc cộng hưởng ở tần số xấp xỉ bằng 1,275Hz (dựa theo đồ thị). Lúc đó tần số góc cộng hưởng của dao động điều hòa
ω = k m ⇒ k ≈ 13 , 64 N / m

Đáp án A
+ Từ đồ thị ta thấy tần số khi xảy ra cộng hưởng ở gần giữa của tần số f1 = 1,25 HZ và .
+ Khoảng rộng một ô trên trục tần số ứng với 0,05Hz
+ Vậy tần số khi có cộng hưởng là:
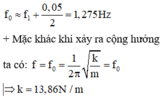

Cái này hình như bạn viết nhầm đơn vị của g phải là m/s2
Khi lò xo có chiều dài l=28 thì vận tốc bằng 0=> vật ở vị trí biên âm
△l=|△l0-A|=2cm
Fd=k|△l|=2N
=>k=100N/m
△l0=\(\dfrac{m.g}{k}\)=0,02(m)=2cm
=>A=4cm
W=1/2.k.A2=0,08j

Chọn trục toạ độ có gốc ở VTCB, chiều dương hướng sang phải.
Phương trình dao động tổng quát là: \(x=A\cos(\omega t+\varphi)\)
Theo thứ tự, ta lần lượt tìm \(\omega;A;\varphi\)
+ \(\omega=\sqrt{\dfrac{k}{m}}=20\sqrt 2(rad/s)\)
+ Biên độ A: \(A^2=x^2+\dfrac{v^2}{\omega^2}=3^2+\dfrac{(80\sqrt 2)^2}{(20\sqrt 2)^2}\)
\(\Rightarrow A = 5cm\)
+ Ban đầu ta có \(x_0=3cm\); \(v_0=-80\sqrt 2\) (cm/s) (do ta đẩy quả cầu về VTCB ngược chiều dương trục toạ độ)
\(\cos\varphi=\dfrac{x_0}{A}=\dfrac{3}{5}\); có \(v_0<0 \) nên \(\varphi > 0\)
\(\Rightarrow \varphi \approx0,3\pi(rad)\)
Vậy PT dao động: \(x=5\cos(20\sqrt 2+0,3\pi)(cm)\)



Giải thích: Đáp án A
Phương pháp: Sử dụng lí thuyết về điều kiện xảy ra cộng hưởng của dao động cưỡng bức và kĩ năng đọc đồ thị
Cách giải:
Khi f nằm trong khoảng từ 1,25Hz đến 1,3Hz thì biên độ cực đại, khi đó xảy ra cộng hưởng.
Thay vào công thức tính tần số ta thu được giá trị xấp xỉ của k = 13,64N/m