K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
a) Áp dụng công thức nhị thức Newton, ta có:
\(\begin{array}{l}{\left( {1 + x} \right)^4} = {1^4} + C_4^1{.1^3}x + C_4^2{.1^2}{x^2} + C_4^3.1{x^3} + C_4^4{x^4}\\ = 1 + 4x + 6{x^2} + 4{x^3} + {x^4}\end{array}\)
\(\begin{array}{l}{\left( {1 - x} \right)^4} = {1^4} + C_4^1{.1^3}\left( { - x} \right) + C_4^2{.1^2}{\left( { - x} \right)^2} + C_4^3.1{\left( { - x} \right)^3} + C_4^4{\left( { - x} \right)^4}\\ = 1 - 4x + 6{x^2} - 4{x^3} + {x^4}\end{array}\)
Suy ra
\(\begin{array}{l}{\left( {1 + x} \right)^4} + {\left( {1 - x} \right)^4} = 1 + 4x + 6{x^2} + 4{x^3} + {x^4} + 1 - 4x + 6{x^2} - 4{x^3} + {x^4}\\ = 2 + 12{x^2} + 2{x^4}\end{array}\)
Vậy \({\left( {1 + x} \right)^4} + {\left( {1 - x} \right)^4} = 2 + 12{x^2} + 2{x^4}\)
Ta có: \(1,{05^4} + 0,{95^4} = {\left( {1 + 0,05} \right)^4} + {\left( {1 - 0,05} \right)^4}\)
Áp dụng biểu thức vừa chứng minh \({\left( {1 + x} \right)^4} + {\left( {1 - x} \right)^4} = 2 + 12{x^2} + 2{x^4}\)
ta có: \(1,{05^4} + 0,{95^4} = {\left( {1 + 0,05} \right)^4} + {\left( {1 - 0,05} \right)^4} = 2 + 12.0,0{5^2} + 2.0,0{5^4}\\ = 2,0300125\)
QT
1
HQ
Hà Quang Minh
Giáo viên
28 tháng 9 2023
a) \({\left( {x + 1} \right)^5} = {x^5} + 5.{x^4}.1 + 10.{x^3}{.1^2} + 10.{x^2}{.1^3} + 5.{x^1}{.1^4} +{1^5} = {x^5} + 5{x^4} + 10{x^3} + 10{x^2} + 5x + 1\)
b) \(\begin{array}{l}{\left( {x - 3y} \right)^5} = {\left[ {x + \left( { - 3y} \right)} \right]^5} = {x^5} + 5{x^4}{\left( { - 3y} \right)^1} + 10{x^3}{\left( { - 3y} \right)^2} + 10{x^2}{\left( { - 3y} \right)^3} + 5{x^1}{\left( { - 3y} \right)^4} + {\left( { - 3y} \right)^5}\\ = {x^5} - 15{x^4}y + 90{x^3}{y^2} - 270{x^2}{y^3} + 405x{y^4} - 243{y^5}\end{array}\)
QT
1
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
a) \({\left( {x - 2} \right)^4}\)
\(\begin{array}{l} = {x^4} + 4{x^3}.\left( { - 2} \right) + 6{x^2}.{\left( { - 2} \right)^2} + 4x{\left( { - 2} \right)^3} + {\left( { - 2} \right)^4}\\ = {x^4} - 8{x^3} + 24{x^2} - 32x + 16\end{array}\)
b) \({\left( {x + 2y} \right)^5}\)
\(\begin{array}{l} = {x^5} + 5.{x^4}.\left( {2y} \right) + 10.{x^3}.{\left( {2y} \right)^2} + 10.{x^2}.{\left( {2y} \right)^3} + 5.x.{\left( {2y} \right)^4} + 1.{\left( {2y} \right)^5}\\ = {x^5} + 10{x^4}y + 40{x^3}{y^3} + 80{x^2}{y^3} + 80x{y^4} + 32{y^5}\end{array}\)
ND
1
15 tháng 4 2023
Hệ số của x^4 sẽ là tổng của 2*a và 1*b, với a là hệ số của x^3 trong (x-1)^5, b là hệ số của x^4 trong (x-1)^5
SHTQ là: \(C^k_5\cdot x^{5-k}\cdot\left(-1\right)^k=C^k_5\cdot\left(-1\right)^k\cdot x^{5-k}\)
Số hạng chứa x^3 tương ứng với 5-k=3
=>k=2
=>Hệ số là \(C^2_5\cdot\left(-1\right)^2=10\)
Số hạng chứa x^4 tương ứng với 5-k=4
=>k=1
=>Hệ số là \(C^1_5\cdot\left(-1\right)=-5\)
=>Hệ số của x^4 là: 2*10+1*(-5)=20-5=15
HQ
Hà Quang Minh
Giáo viên
28 tháng 9 2023
+) Ta có:
\(\begin{array}{l}{\left( {3x + 2} \right)^5} = {\left( {3x} \right)^5} + 5.{\left( {3x} \right)^4}2 + 10.{\left( {3x} \right)^3}{2^2} + 10{\left( {3x} \right)^2}{.2^3} + 5.\left( {3x} \right){.2^4} + {2^5}\\ = 243{x^5} + 810{x^4} + 1080{x^3} + 720{x^2} + 240x + 32\end{array}\)
+) Hệ số của \({x^4}\) trong khai triển trên là: \({a_4} = 810\)
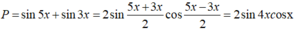
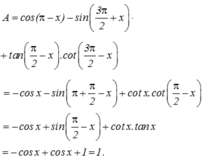
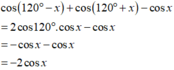
TK:
Để khai triển biểu thức \((x - 5)^4\), ta có thể sử dụng công thức khai triển Newton hoặc sử dụng quy tắc nhị thức của Pascal. Tuy nhiên, trong trường hợp này, để đơn giản, chúng ta có thể sử dụng quy tắc nhị thức để thực hiện khai triển:
Bằng quy tắc nhị thức, ta có:
\[(x - 5)^4 = \binom{4}{0}x^4(-5)^0 + \binom{4}{1}x^3(-5)^1 + \binom{4}{2}x^2(-5)^2 + \binom{4}{3}x^1(-5)^3 + \binom{4}{4}x^0(-5)^4\]
\(= x^4 + \binom{4}{1}x^3(-5) + \binom{4}{2}x^2(25) + \binom{4}{3}x(-125) + (-5)^4\)
\(= x^4 - 20x^3 + 100x^2 - 500x + 625\)
Vậy kết quả của khai triển biểu thức \((x - 5)^4\) là \(x^4 - 20x^3 + 100x^2 - 500x + 625\).