Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số sản phẩm đội dự định làm mỗi ngày là x (x ∈ ℕ * , x < 84) (sản phẩm)
*) Theo kế hoạch, thời gian hoàn thành là 1000/x (ngày)
*) Thực tế, mỗi ngày làm được x + 10 (sản phẩm)
Thời gian hoàn thành 1000/(x+10) (ngày)
Vì thời gian thực tế ít hơn thời gian dự định là 2 ngày nên ta có phương trình:
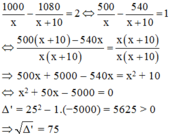
Phương trình có hai nghiệm phân biệt: x 1 = − 25 – 75 = −100 (loại)
và x 2 = −25 + 75 = 50 (tmđk)
Vậy theo kế hoạch, mỗi ngày tổ dự định làm 50 sản phẩm
Đáp án: C

Đổi 30 phút =1/2 h
Gọi năng suất người công nhân theo kế hoạch là x(sản phâm/h) ĐK: \(x>0,x\in N\)
Theo kế hoạch thì thời gian mà người đó hoàn thành 60sp là \(\frac{60}{x}\left(h\right)\)
Nhưng trên thực tế người công nhân đó mỗi giờ làm thêm 2 sản phẩm vậy năng suất thự tế là \(x+2\)(sp/h)
Số sản phẩm mà người đó làm được trên thực tế là \(60+3=63\left(sp\right)\)
Do đó thời gian thực tế mà người đó hoàn thành công việc là \(\frac{63}{x+2}\left(h\right)\)
Vì kế hoạch được hoàn thành sớm hơn dự định 1/2 h nên ta có pt sau:
\(\frac{60}{x}-\frac{63}{x+2}=\frac{1}{2}\)
\(\Leftrightarrow\frac{60x+120}{x\left(x+2\right)}-\frac{63x}{x\left(x+2\right)}=\frac{1}{2}\)
\(\Leftrightarrow\frac{-3x+120}{x^2+2x}=\frac{1}{2}\)
\(\Leftrightarrow x^2+2x=-6x+240\)
\(\Leftrightarrow x^2+8x-240=0\)
\(\Leftrightarrow x^2-12x+20x-240=0\)
\(\Leftrightarrow x\left(x-12\right)+20\left(x-12\right)=0\)
\(\Leftrightarrow\left(x-12\right)\left(x+20\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=12\left(tm\right)\\x=-20\left(loai\right)\end{cases}}\)
Vậy theo kế hoạch mỗi giờ người đó làm được 12 sản phẩm
Gọi số sản phẩm người đó phải hoàn thành theo kế hoạch trong mỗi giờ là a (sản phẩm) (a>0)
Nên số giờ người đó dự định hoàn thành 60 sản phẩm là \(\frac{60}{a}\) (giờ)
Do cải tiến kĩ thuật nên mỗi giờ người đó làm được a+2 (sản phẩm), và còn vượt mức 3 sản phẩm nên thời gian hoàn thành công việc thực tế là \(\frac{60+3}{a+2}\left(giờ\right)\)
Sớm hơn dự định 30 phút = \(\frac{1}{2}\) giờ, nên ta có:
\(\frac{60}{a}-\frac{60+3}{a+2}=\frac{1}{2}\)
\(\Rightarrow\left[60\left(a+2\right)-63a\right]2=a^2+2a\)
\(\Rightarrow a^2+8a-240=0\)
\(\Delta'=4^2+240=256>0\)
\(\Rightarrow a=-4-\sqrt{256}=-20< 0\left(l\right)\)
Hoặc \(a=-4+\sqrt{256}=12\) ( nhận )
Vậy theo kế hoạch mỗi giờ người đó làm 12 sản phẩm.

Gọi số sản phẩm người đó mỗi giờ phải làm theo kế hoạch là \(x\)(sản phẩm), \(x>0\).
Theo kế hoạch người đó hoàn thành công việc sau số giờ là: \(\frac{60}{x}\)(giờ)
Đổi: \(30\)phút \(=\)\(0,5\)giờ.
Thực tế mỗi giờ người đó sản xuất được: \(x+2\)(sản phẩm)
Người đó hoàn thành công việc sau: \(\frac{60}{x}-0,5\)(giờ).
Ta có phương trình:
\(\left(x+2\right)\left(\frac{60}{x}-0,5\right)=63\)
\(\Rightarrow-0,5x^2+59x+120=63x\)
\(\Leftrightarrow x^2+8x-240=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=12\left(tm\right)\\x=-20\left(l\right)\end{cases}}\)

Gọi năng suất làm việc theo dự kiến của xí nghiệp là x(sản phẩm/ngày), (x > 4)
+) Theo dự kiến: Mỗi ngày phân xưởng sản xuất x sản phẩm, tổng sản phẩm là 200 sản phẩm và thời gian sản xuất là 200/x ngày
+ Thực tế: 5 ngày đầu phân xưởng sản xuất x – 4 (sản phẩm/ngày), số sản phẩm sản xuất được là 5 (x – 4). Những ngày sau mỗi ngày phân xưởng sản xuất x + 10 (sản phẩm/ngày), số sản phẩm sản xuất được là 220 – 5x với thời gian sản xuất là 220 - 5 x x + 10 (ngày)
*) Vì thực tế xí nghiệp đã hoàn thành công việc sớm hơn 1 ngày so với dự định nên ta có phương trình:
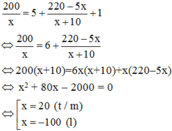
Vậy theo dự kiến mỗi ngày phân xưởng sản xuất 20 sản phẩm
Đáp án: D

Gọi x là sản ppham xưởng sản xuất trong 1 ngày theo kế hoạch (x>0)
=>Số ngày theo kế hoạch là :\(\frac{110}{x}\)
Số ngày thực tế là \(\frac{1100}{x+5}\)theo gia thiet cua bai toan ta co :
\(\frac{1100}{x}-\frac{1100}{x+5}=2\)
<=>1100(x+5)-1100x=2x(x+5)
<=>2x^2+10x-5500=0
<=>x=50hay x=-55 loai
Vậy theo kế hoạch mỗi ngày phân xưởng phải sản xuất là 50 sản phẩm
Gọi số sản phẩm mà phân xưởng làm trong 1 ngày là x ( x > 0 )
=> Số ngày quy định = \(\frac{1100}{x}\)( ngày )
Mỗi ngày phân xưởng sản xuất vượt mức 5 sản phẩm
=> Số ngày hoàn thành = \(\frac{1100}{x+5}\)( ngày )
Vì thế kế hoạch hoàn thành sớm hơn quy định 2 ngày
=> Ta có phương trình : \(\frac{1100}{x}-\frac{1100}{x+5}=2\)
\(\Leftrightarrow\frac{1100\left(x+5\right)}{x\left(x+5\right)}-\frac{1100\cdot x}{x\left(x+5\right)}=\frac{2x\left(x+5\right)}{x\left(x+5\right)}\)
\(\Leftrightarrow1100x+5500-1100x=2x^2+10x\)
\(\Leftrightarrow2x^2+10x-1100x-5500+1100x=0\)
\(\Leftrightarrow2x^2+10x-5500=0\)
\(\Delta'=b'^2-ac=5^2-2\cdot\left(-5500\right)=25+11000=11025\)
\(\Delta'>0\)nên phương trình đã cho có hai nghiệm phân biệt :
\(\hept{\begin{cases}x_1=\frac{-b'+\sqrt{\Delta'}}{a}=\frac{-5+\sqrt{11025}}{2}=50\\x_2=\frac{-b-\sqrt{\Delta'}}{a}=\frac{-5-\sqrt{11025}}{2}=-55\end{cases}}\)
x > 0 => x = 50
Vậy theo kế hoạch , mỗi ngày phân xưởng sản xuất 50 sản phẩm

Gọi số sản phẩm làm theo kế hoạch mỗi ngày là x>0 và số ngày dự định là y>0
Ta có: \(xy=200\)
4 ngày đầu làm được: \(4x\) sản phẩm
Những ngày còn lại: \(\left(y-6\right)\left(x+10\right)\)
Theo bài ra ta có hệ:
\(\left\{{}\begin{matrix}xy=200\\4x+\left(y-6\right)\left(x+10\right)=200\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy=200\\5y-x=30\end{matrix}\right.\)
\(\Rightarrow y\left(5y-30\right)=200\)
\(\Leftrightarrow y^2-6y-40=0\Rightarrow\left[{}\begin{matrix}y=10\\y=-4\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow x=\dfrac{200}{10}=20\)

Gọi x là số sản phẩm mỗi giờ mà người công nhân phải hoàn thành theo kế hoạch
(x ∈ ℕ * , x < 84)
Số sản phẩm mỗi giờ mà người công nhân phải hoàn thành theo thực tế: x + 2
Thời gian mà công nhân hoàn thành theo kế hoạch: 84/x (h)
Thời gian mà công nhân hoàn thành theo thực tế: 84/(x+2) (h)
Người công nhân đó hoàn thành công việc sớm hơn dự định 1 giờ nên ta có phương trình:
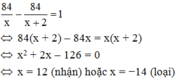
Vậy theo kế hoạch mỗi giờ người công nhân phải làm 12 sản phẩm
Đáp án: B
gọi x là số sản phẩm mỗi ngày làm đc theo kế hoạch (x ∈ N*)
số ngày dự định làm 600 sản phẩm là: \(\dfrac{600}{x}\left(ngày\right)\)
vì có cải tiến kĩ thuật nên năng suất mỗi ngày tăng 10 sản phẩm nên: x + 10 (sản phẩm)
cơ sở đã hoàn thành sớm 1 ngày nên: \(\dfrac{600}{x}-1\left(ngày\right)\)
theo đề ta có phương trình:
\(\left(x+10\right)\cdot\left(\dfrac{600}{x}-1\right)=700\\ \left(x+10\right)\left(600-x\right)=700x\\ 600x-x^2+6000-10x=700x\\ -x^2+590x+6000=700x\\ -x^2+590x+6000-700x=0\\ x^2+110x-6000=0\\ =>x=\left\{{}\begin{matrix}40\left(TM\right)\\-150\left(KTM\right)\end{matrix}\right.\)
vậy theo kế hoạch mỗi ngày phải làm 40 sản phẩm