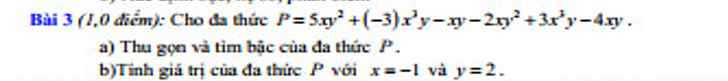Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Để x2 - 8 / x - 1 thuộc Z thì x2 - 8 chia hết cho x - 1
=> x2 - x + x - 1 - 7 chia hết cho x - 1
=> x . (x - 1) + (x - 1) - 7 chia hết cho x - 1
=> (x - 1) . (x + 1) - 7 chia hết cho x - 1
Vì (x - 1) . (x + 1) chia hết cho x - 1 nên 7 chia hết cho x - 1
Do x thuộc Z nên x - 1 thuộc Z => x - 1 thuộc { 1 ; -1 ; 7 ; -7}
=> x thuộc { 2 ; 0 ; 8 ; -6}
Vậy x thuộc [ 2 ; 0 ; 8 ; -6}
Để x2 - 8 / x - 1 thuộc Z thì x2 - 8 chia hết cho x - 1
=> x2 - x + x - 1 - 7 chia hết cho x - 1
=> x . (x - 1) + (x - 1) - 7 chia hết cho x - 1
=> (x - 1) . (x + 1) - 7 chia hết cho x - 1
Vì (x - 1) . (x + 1) chia hết cho x - 1 nên 7 chia hết cho x - 1
Do x thuộc Z nên x - 1 thuộc Z => x - 1 thuộc { 1 ; -1 ; 7 ; -7}
=> x thuộc { 2 ; 0 ; 8 ; -6}
Vậy x thuộc [ 2 ; 0 ; 8 ; -6}

A B C M
b)Xét \(\Delta ABM và \Delta ACM\) có:
\(AB=AC\)
\(AM\) chung
\(BM=CM\)
\(\Rightarrow\)\(\Delta ABM=\Delta ACM\) (c-c-c)
b)Vì\(\Delta ABM=\Delta ACM\) nên \(\widehat{B}=\widehat{C}\)
Ta có: M là trung điểm của cạnh BC nên BM = CM
a) Xét △ ABM và △ ACM ta có:
AB = AC ( gt )
AM cạnh chung
BM = CM ( cmt )
⇒ △ ABM = △ ACM ( c - g - c ) ( 1 )
b) Cách 1:
Vì AB = AC nên △ ABC là tam giác cân
⇒ \(\widehat{B}=\widehat{C}\) ( đpcm )
Cách 2:
Từ (1) suy ra: \(\widehat{B}=\widehat{C}\) ( 2 góc tương ứng )

\(a,P=5xy^2+\left(-3\right)x^2y-xy-2xy^2+3x^2y-4xy=3xy^2-5xy\)
Bậc: 3
b, Thay x=-1, y=2 vào pt ta có:
\(P=3xy^2-5xy=3.\left(-1\right).2^2-5.\left(-1\right).2=-3.4+5.2=-12+10=-2\)