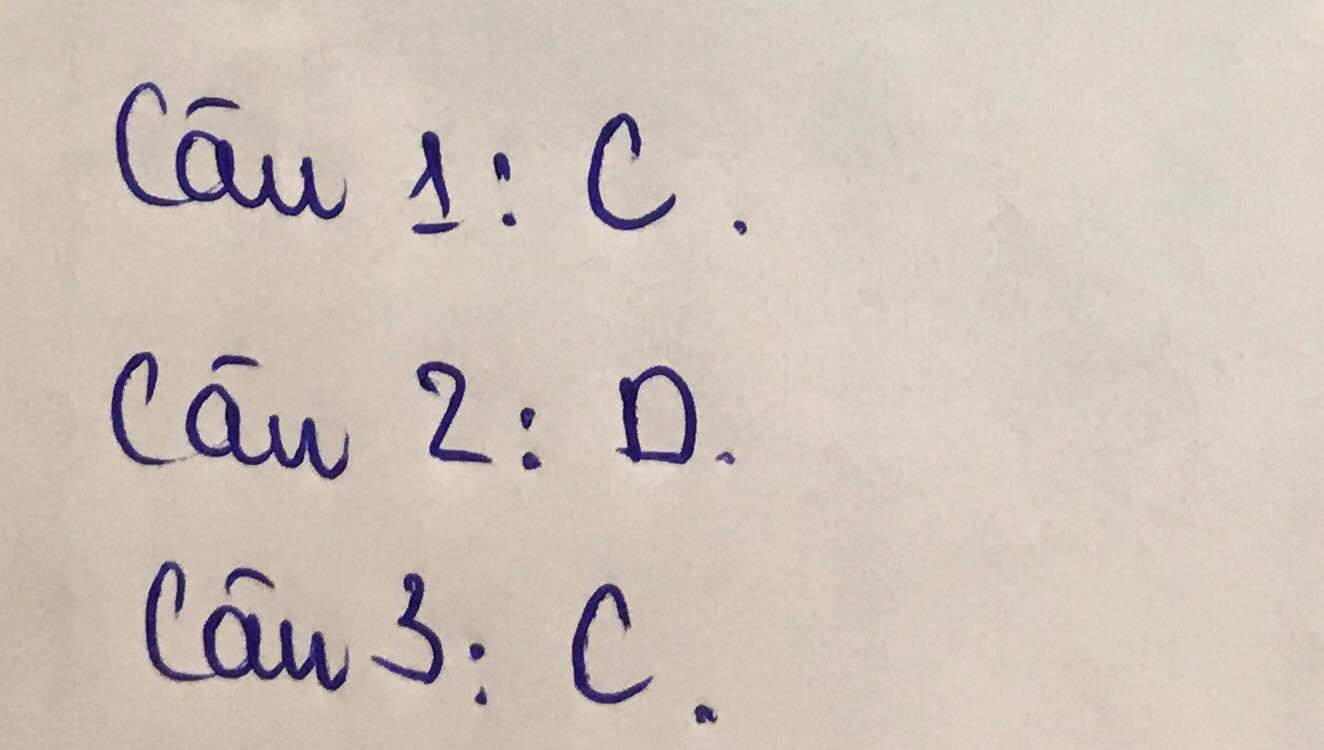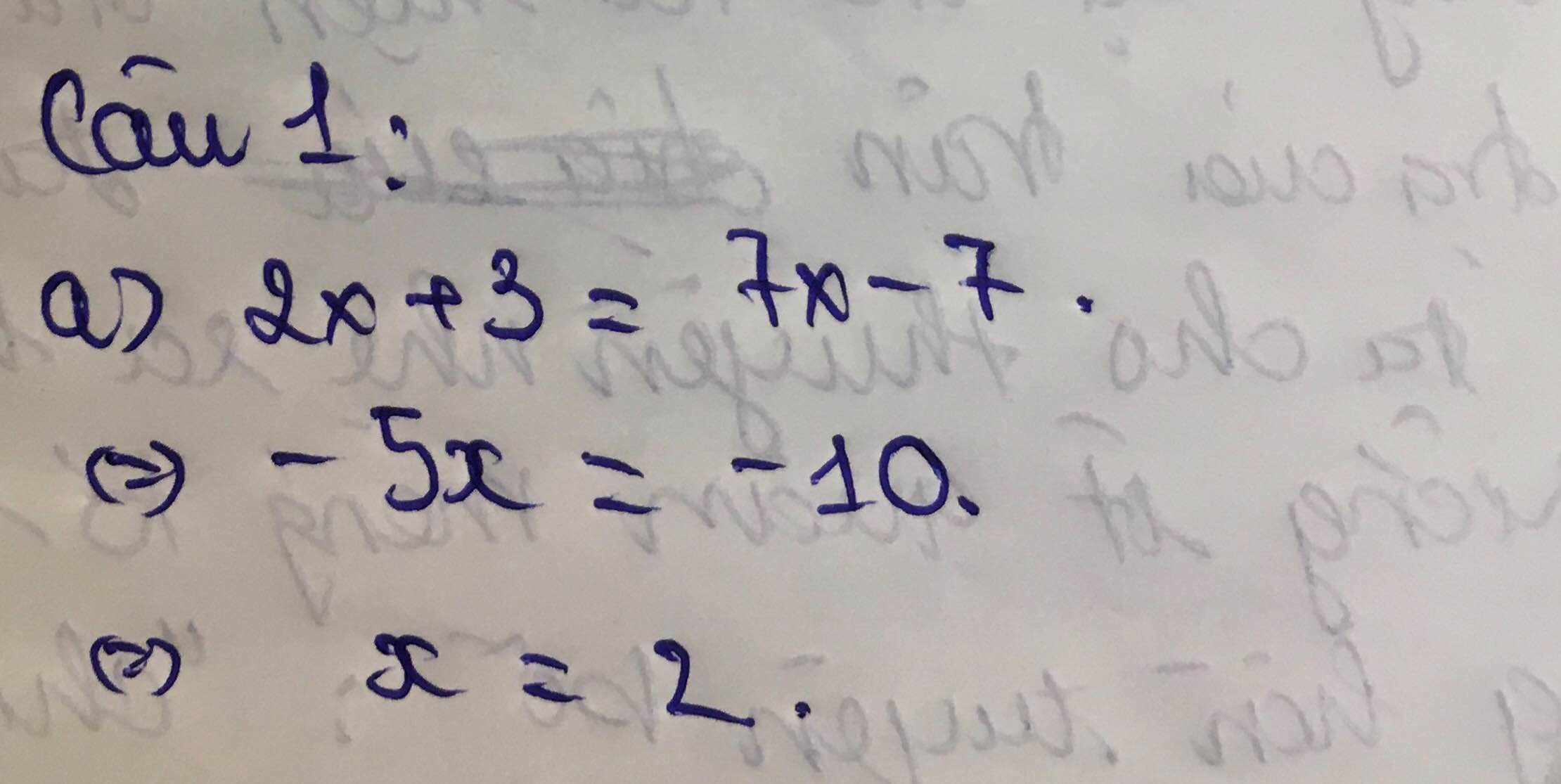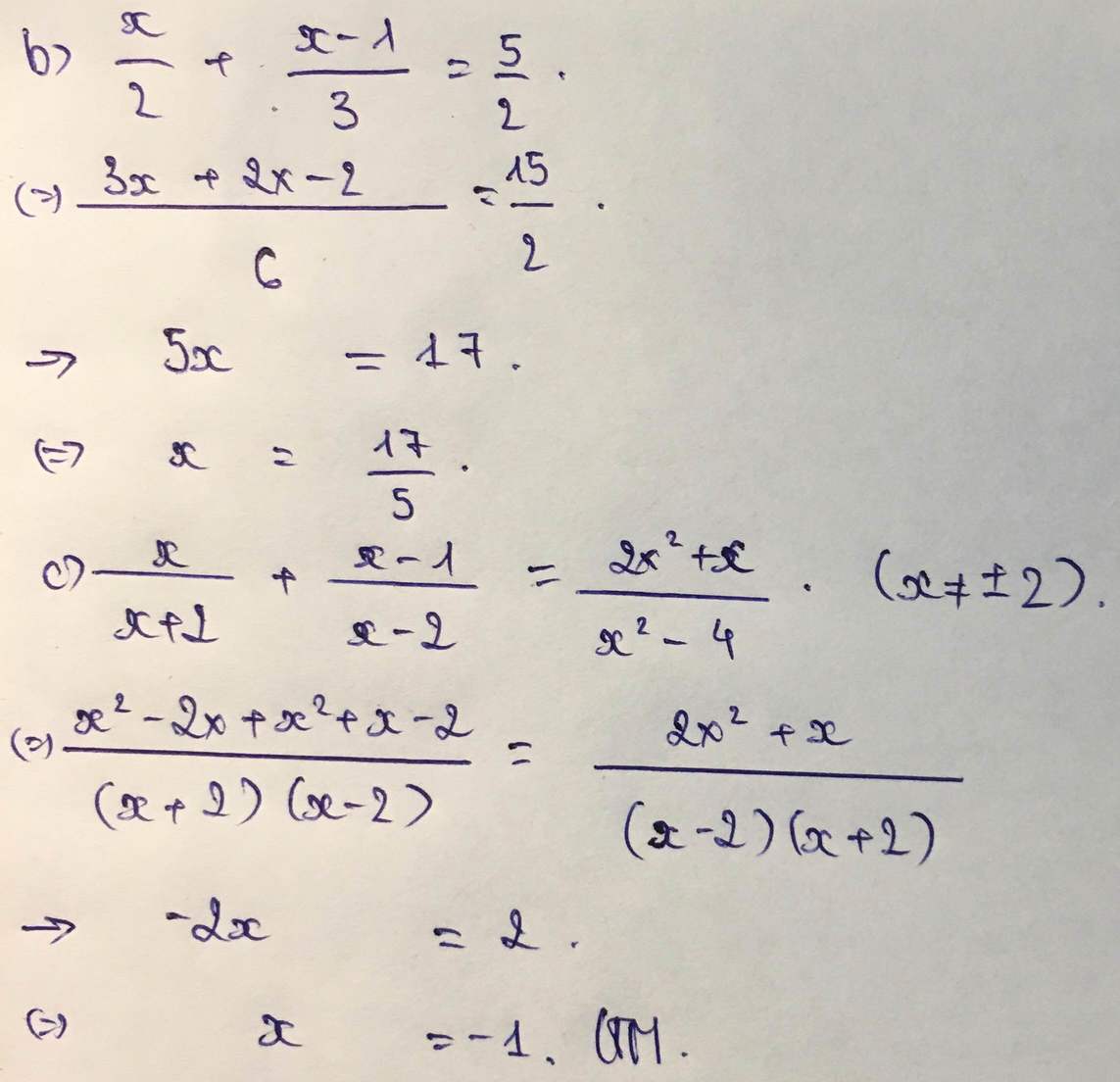Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Đúng
b)Đúng
c)Sai vì nghiệm không thỏa mãn ĐKXĐ
d)Sai vì có 1 nghiệm không thỏa mãn ĐKXĐ

Câu 1a : tự kết luận nhé
\(2\left(x+3\right)=5x-4\Leftrightarrow2x+6=5x-4\Leftrightarrow-3x=-10\Leftrightarrow x=\frac{10}{3}\)
Câu 1b : \(\frac{1}{x-3}-\frac{2}{x+3}=\frac{5-2x}{x^2-9}\)ĐK : \(x\ne\pm3\)
\(\Leftrightarrow x+3-2x+6=5-2x\Leftrightarrow-x+9=5-2x\Leftrightarrow x=-4\)
c, \(\frac{x+1}{2}\ge\frac{2x-2}{3}\Leftrightarrow\frac{x+1}{2}-\frac{2x-2}{3}\ge0\)
\(\Leftrightarrow\frac{3x+3-4x+8}{6}\ge0\Rightarrow-x+11\ge0\Leftrightarrow x\le11\)vì 6 >= 0
1) 2(x + 3) = 5x - 4
<=> 2x + 6 = 5x - 4
<=> 3x = 10
<=> x = 10/3
Vậy x = 10/3 là nghiệm phương trình
b) ĐKXĐ : \(x\ne\pm3\)
\(\frac{1}{x-3}-\frac{2}{x+3}=\frac{5-2x}{x^2-9}\)
=> \(\frac{x+3-2\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}=\frac{5-2x}{\left(x-3\right)\left(x+3\right)}\)
=> x + 3 - 2(x - 3) = 5 - 2x
<=> -x + 9 = 5 - 2x
<=> x = -4 (tm)
Vậy x = -4 là nghiệm phương trình
c) \(\frac{x+1}{2}\ge\frac{2x-2}{3}\)
<=> \(6.\frac{x+1}{2}\ge6.\frac{2x-2}{3}\)
<=> 3(x + 1) \(\ge\)2(2x - 2)
<=> 3x + 3 \(\ge\)4x - 4
<=> 7 \(\ge\)x
<=> x \(\le7\)
Vậy x \(\le\)7 là nghiệm của bất phương trình
Biểu diễn
-----------------------|-----------]|-/-/-/-/-/-/>
0 7

Câu 1: (3,0 điểm). Giải các phương trình:
a) \(3x+5=2x+2\).
\(\Leftrightarrow3x-2x=2-5\).
\(\Leftrightarrow x=-3\).
Vậy phương trình có tập nghiệm: \(S=\left\{-3\right\}\).
b) \(\frac{x-5}{\left(x+1\right)\left(x-2\right)}=\frac{4}{x+1}+\frac{3}{x-2}\left(ĐKXĐ:x\ne-1;x\ne2\right)\).
\(\Leftrightarrow\frac{x-5}{\left(x+1\right)\left(x-2\right)}=\frac{4\left(x-2\right)}{\left(x+1\right)\left(x-2\right)}+\frac{3\left(x+1\right)}{\left(x+1\right)\left(x-2\right)}\).
\(\Rightarrow x-5=4x-8+3x+3\).
\(\Leftrightarrow x-4x-3x=-8+3+5\).
\(\Leftrightarrow-6x=0\).
\(\Leftrightarrow x=0\)(thỏa mãn ĐKXĐ).
Vậy phương trình có tập nghiệm: \(S=\left\{0\right\}\).
c) \(\left|x-3\right|+1=2x-7\)
- Xét \(x-3\ge0\Leftrightarrow x\ge3\). Do đó \(\left|x-3\right|=x-3\). Phương trình trở thành:
\(x-3+1=2x-7\).
\(\Leftrightarrow x-2=2x-7\).
\(\Leftrightarrow x-2x=-7+2\).
\(\Leftrightarrow-x=-5\).
\(\Leftrightarrow x=5\)(thỏa mãn).
- Xét \(x-3< 0\Leftrightarrow x< 3\)Do đó \(\left|x-3\right|=3-x\). Phương trình trở thành:
\(3-x+1=2x-7\).
\(\Leftrightarrow4-x=2x-7\).
\(-x-2x=-7-4\).
\(\Leftrightarrow-3x=-11\).
\(\Leftrightarrow x=\frac{-11}{-3}=\frac{11}{3}\)(loại).
Vậy phương trình có tập nghiệm: \(S=\left\{5\right\}\).
Câu 2: (2,0 điểm).
a) \(5x-5>x+15\).
\(\Leftrightarrow5x-x>15+5\).
\(\Leftrightarrow4x>20\).
\(\Leftrightarrow x>5\).
Vậy bất phương trình có tập nghiệm: \(\left\{x|x>5\right\}\).
b) \(\frac{8-4x}{3}>\frac{12-x}{5}\).
\(\Leftrightarrow\frac{5\left(8-4x\right)}{15}>\frac{3\left(12-x\right)}{15}\).
\(\Leftrightarrow40-20x>36-3x\).
\(\Leftrightarrow-20x+3x>36-40\).
\(\Leftrightarrow-17x>-4\).
\(\Leftrightarrow x< \frac{4}{17}\)\(\Leftrightarrow x< 0\frac{4}{17}\).
\(\Rightarrow\)Số nguyên x lớn nhất thỏa mãn bất phương trình trên là: \(x=0\).
Vậy \(x=0\).

1a)
\(\hept{\begin{cases}2x-2017=1\\12x-2017=1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2x=2018\\12x=2018\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=1009\\x=\frac{1009}{6}\end{cases}}\)
Em nghĩ là như vậy . Nếu có gì em sẽ sửa.
Gọi số thứ nhất là a ( 0 < a < 125 )
Số thứ hai là 4a
Ta có phương trình :
\(a+4a=125\)
\(\Leftrightarrow5a=125\)
\(\Leftrightarrow a=25\left(tm\right)\)
Vậy số thứ 1 là 25
Số thứ 2 = 25 x 4 = 100
Vậy ...

a)
\(\dfrac{x-3}{5}+\dfrac{1-2x}{3}=6\\ < =>3x-9+5-10x=90\)
\(< =>3x-10x=90+9-5\\ < =>-7x=94\\ < =>x=-\dfrac{94}{7}\)
b)
\(\left(2x-3\right)\left(x^2+1\right)=0\\ < =>\left[{}\begin{matrix}2x-3=0\\x^2+1=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=\dfrac{3}{2}\\x^2=-1\left(voli\right)\end{matrix}\right.\\ < =>x=\dfrac{3}{2}\)
c)
\(\dfrac{2}{x+1}-\dfrac{1}{x-2}=\dfrac{3x-11}{\left(x+1\right)\left(x-2\right)}\left(x\ne-1;x\ne2\right)\)
suy ra: \(2\left(x-2\right)-x-1=3x-11\)
\(< =>2x-4-x-1-3x+11=0\)
\(< =>2x-x-3x=4+1-11\\ < =>-2x=-6\\ < =>x=3\left(tm\right)\)
a) \(\dfrac{x-3}{5}+\dfrac{1-2x}{3}=6\)
\(\Leftrightarrow3\left(x-3\right)+5\left(1-2x\right)=90\)
\(\Leftrightarrow-4-7x=90\)
\(\Leftrightarrow x=-\dfrac{94}{7}\)
b) \(\left(2x-3\right)\left(x^2+1\right)=0\)
\(\Leftrightarrow2x-3=0\) (Vì \(x^2+1>0\))
\(\Leftrightarrow x=\dfrac{3}{2}\)
c) \(\dfrac{2}{x+1}-\dfrac{1}{x-2}=\dfrac{3x-11}{\left(x+1\right)\left(x-2\right)}\left(Đk:x\ne-1;x\ne2\right)\)
\(\Leftrightarrow2\left(x-2\right)-\left(x+1\right)=3x-11\)
\(\Leftrightarrow x-5=3x-11\)
\(\Leftrightarrow x=3\)

Bài 1:
a) \(x^3-5x^2+8x-4\)
\(=x^3-4x^2+4x-x^2+4x-4\) \(=x\left(x^2-4x+4\right)-\left(x^2-4x+4\right)\)\(=\left(x-1\right)\left(x-2\right)^2\)
b) Ta có: \(\frac{A}{M}=\frac{10x^2-7x-5}{2x-3}=5x+4+\frac{7}{2x-3}\)
Với \(x\in Z\)thì \(A⋮M\)khi \(\frac{7}{2x-3}\in Z\)\(\Rightarrow7⋮\left(2x-3\right)\)\(\Rightarrow2x-3\inƯ\left(7\right)=\left\{\pm1;\pm7\right\}\)
\(\Rightarrow=\left\{1;5;\pm2\right\}\)thì khi đó \(A⋮M\)
Các bài làm này có đúng ko ạ, ai đó duyệt giúp em, em cảm ơn.
Bài 1:
a)x3-5x2+8x-4=x3-4x2+4x-x2+4x-4
=x(x2-4x-4)-(x2-4x+4)
=(x-1) (x-2)2
b)Xét:
\(\frac{a}{b}-\frac{10x^2-7x-5}{2x-3}\)
=\(5x+4+\frac{7}{2x-3}\)
Với x thuộc Z thì A /\ B khi \(\frac{7}{2x-3}\) thuộc Z => 7 /\ (2x-3)
Mà Ư(7)={-1;1;-7;7} => x=5;-2;2;1 thì A /\ B
c)Biến đổi \(\frac{x}{y^3-1}-\frac{x}{x^3-1}=\frac{x^4-x-y^4+y}{\left(y^3-1\right)\left(x^3-1\right)}\)
=\(\frac{\left(x^4-y^4\right)\left(x-y\right)}{xy\left(y^2+y+1\right)\left(x^2+x+1\right)}\)(do x+y=1=>y-1=-x và x-1=-y)
=\(\frac{\left(x-y\right)\left(x+y\right)\left(x^2+y^2\right)-\left(x-y\right)}{xy\left[x^2y^2+y^2x+y^2+xy^2+xy+y+x^2+x+1\right]}\)
=\(\frac{\left(x-y\right)\left(x^2+y^2-1\right)}{xy\left[x^2y^2+xy\left(x+y\right)+x^2+y^2+xy+2\right]}\)
=\(\frac{\left(x-y\right)\left(x^2-x+y^2-y\right)}{xy\left[x^2y^2+\left(x+y\right)^2+2\right]}=\frac{\left(x-y\right)\left[x\left(x-1\right)+y\left(y-1\right)\right]}{xy\left(x^2y^2+3\right)}\)
=\(\frac{\left(x-y\right)\left[x\left(-y\right)+y\left(-x\right)\right]}{xy\left(x^2y^2+3\right)}=\frac{\left(x-y\right)\left(-2xy\right)}{xy\left(x^2y^2+3\right)}\)
=\(\frac{-2\left(x-y\right)}{x^2y^2+3}\)Suy ra điều phải chứng minh
Bài 2 )
a)(x2+x)2+4(x2+x)=12 đặt y=x2+x
y2+4y-12=0 <=>y2+6y-2y-12=0
<=>(y+6)(y-2)=0 <=> y=-6;y=2
>x2+x=-6 vô nghiệm vì x2+x+6 > 0 với mọi x
>x2+x=2 <=> x2+x-2=0 <=> x2+2x-x-2=0
<=>x(x+2)-(x+2)=0 <=>(x+2)(x-1) <=> x=-2;x-1
Vậy nghiệm của phương trình x=-2;x=1
b)\(\frac{x+1}{2008}+\frac{x+2}{2007}+\frac{x+3}{2006}+\frac{x+4}{2005}+\frac{x+5}{2004}\)\(+\frac{x+6}{2003}\)
=\(\left(\frac{x+1}{2008}+1\right)+\left(\frac{x+2}{2007}+1\right)+\left(\frac{x+3}{2006}+1\right)+\left(\frac{x+4}{2005}+1\right)\)\(+\left(\frac{x+5}{2004}+1\right)+\left(\frac{x+6}{2003}+1\right)\)
<=>\(\frac{x+2009}{2008}+\frac{x+2009}{2007}+\frac{x+2009}{2006}-\frac{x+2009}{2005}\)\(+\frac{x+2009}{2004}+\frac{x+2009}{2003}\)
<=>\(\frac{x+2009}{2008}+\frac{x+2009}{2007}+\frac{x+2009}{2006}\)\(-\frac{x+2009}{2005}-\frac{x+2009}{2004}-\frac{x+2009}{2003}=0\)
Nhờ OLM xét giùm em vs ạ !