K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 2 2023
\(\dfrac{u_5}{u_2}=\dfrac{u_1.q^4}{u_1.q}=q^3=\dfrac{32}{4}=8\)
\(\Rightarrow q=2\)
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 9 2020
\(sina+sinb+sinc+3=0\)
\(\Leftrightarrow\left(sina+1\right)+\left(sinb+1\right)+\left(sinc+1\right)=0\)
Do \(\left\{{}\begin{matrix}sina\ge-1\\sinb\ge-1\\sinc\ge-1\end{matrix}\right.\) ;\(\forall a;b;c\)
\(\Rightarrow\left(sina+1\right)+\left(sinb+1\right)+\left(sinc+1\right)\ge0\)
Dấu "=" xảy ra khi và chỉ khi \(sina=sinb=sinc=-1\)
\(\Rightarrow cosa=cosb=cosc=0\Rightarrow cosa+cosb+cosc+10=10\)
b/ \(sinx=1-sin^2x\Rightarrow sinx=cos^2x\)
\(\Rightarrow sin^2x=cos^4x\Rightarrow1-cos^2x=cos^4x\)
\(\Rightarrow cos^4x+cos^2x=1\Rightarrow\left(cos^4x+cos^2x\right)^2=1\)
\(\Rightarrow cos^8x+2cos^6x+cos^4x=1\)
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 8 2020
Phép vị tự biến tam giác ABC thành AB'C' có diện tích:
\(S_{AB'C'}=k^2S_{ABC}=9.12=108\)
BT
25 tháng 5 2017
a)
Gọi q là công bội của \(\left(u_n\right)\). Ta có:
\(\left\{{}\begin{matrix}u_1+u_1q^4=51\\u_1q+u_1q^5=102\end{matrix}\right.\)\(\Rightarrow\dfrac{u_1+u_1q^4}{u_1q_1+u_1q^5}=\dfrac{51}{102}\)\(\Leftrightarrow\dfrac{1+q^4}{q+q^5}=\dfrac{1}{2}\)\(\Leftrightarrow\dfrac{1+q^4}{q\left(1+q^4\right)}=\dfrac{1}{2}\)\(\Leftrightarrow\dfrac{1}{q}=\dfrac{1}{2}\)\(\Leftrightarrow q=2\).
Suy ra: \(u_1+2^4u_1=51\)\(\Leftrightarrow17u_1=51\)\(\Leftrightarrow u_1=3\).
b) \(S_n=\dfrac{u_1\left(1-q^n\right)}{1-q}=\)\(\dfrac{3\left(1-2^n\right)}{1-2}=3\left(2^n-1\right)=3069\)
\(\Leftrightarrow2^n-1=1023\)\(\Leftrightarrow2^n=1024=2^{10}\)\(\Leftrightarrow n=10\).
Vậy tổng của 10 số hạng đầu tiên bằng 10.
c)
Có \(u_1.q^{n-1}=3.2^{n-1}=12288\)\(\Leftrightarrow2^{n-1}=4096=2^{12}\)\(\Leftrightarrow n-1=12\)\(\Leftrightarrow n=13\).
Vậy số hạng thứ 13 bằng 12 288.
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 3 2021
3.
Đặt \(f\left(x\right)=x^4-3x^3+x-\dfrac{1}{8}\)
Hàm \(f\left(x\right)\) liên tục trên R
Do \(f\left(x\right)\) là đa thức bậc 4 nên có tối đa 4 nghiệm
Ta có: \(f\left(-1\right)=\dfrac{23}{8}>0\)
\(f\left(0\right)=-\dfrac{1}{8}< 0\Rightarrow f\left(-1\right).f\left(0\right)< 0\)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(-1;0\right)\)
\(f\left(\dfrac{1}{2}\right)=\dfrac{1}{16}>0\Rightarrow f\left(0\right).f\left(\dfrac{1}{2}\right)< 0\)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(0;\dfrac{1}{2}\right)\)
\(f\left(1\right)=-\dfrac{9}{8}< 0\Rightarrow f\left(\dfrac{1}{2}\right).f\left(1\right)< 0\)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(\dfrac{1}{2};1\right)\)
\(f\left(3\right)=\dfrac{23}{8}>0\Rightarrow f\left(1\right).f\left(3\right)< 0\)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(1;3\right)\)
Vậy pt có 4 nghiệm thuộc các khoảng nói trên
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 3 2021
4.
\(\lim\limits_{x\rightarrow-\infty}\left(\sqrt{x^2+ax+2017}+x\right)=\lim\limits_{x\rightarrow-\infty}\dfrac{ax+2017}{\sqrt{x^2+ax+2017}-x}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{a+\dfrac{2017}{x}}{-\sqrt{1+\dfrac{a}{x}+\dfrac{2017}{x^2}}-1}=-\dfrac{a}{2}\)
\(\Rightarrow-\dfrac{a}{2}=6\Rightarrow a=-12\)
K
17 tháng 2 2022
ngày 19 là ngày thứ 6 - ngày cuối cùng của tháng 8 - là ngày thứ tư-tháng 8 có tổng cộng 4 ngày chủ nhật
17 tháng 2 2022
• ngày 19 tháng 8 là ngày thứ sáu.
\(\text{• Ngày cuối cùng của tháng 8 là ngày 31 và là ngày thứ tư}\)
• Tháng 8 có bốn ngày chủ nhật. Đó là những ngày: 7, 14, 21, 28 tháng 8
\(\text{• Chủ nhật cuối cùng của tháng 8 là ngày 28 tháng 8}\)
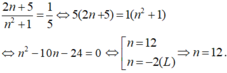
dẹp luôn đi hỏi làm gì nữa
Ghi thế ai trả lời đc bạn ơi