Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

d) \(\frac{5x+2}{6}-\frac{8x-1}{3}=\frac{4x-2}{5}-5\)
\(\Leftrightarrow\frac{5\left(5x+2\right)}{30}-\frac{10\left(8x-1\right)}{30}=\frac{6\left(4x-2\right)}{30}-\frac{150}{30}\)
\(\Leftrightarrow25x+10-80x+10=24x-12-150\)
\(\Leftrightarrow25x-80x-24x=-12-150-10-10\)
\(\Leftrightarrow-79x=-182\)
\(\Leftrightarrow x=\frac{182}{79}\).
Vậy tập nghiệm phương trình \(s=\left\{\frac{182}{79}\right\}\)
a)\(\frac{3x+2}{2}-\frac{3x+1}{6}=\frac{5}{3}+2x\)
\(\Leftrightarrow\frac{3\left(3x+2\right)}{6}-\frac{3x+1}{6}=\frac{10}{6}+\frac{12x}{6}\)
\(\Leftrightarrow9x+6-3x+1=10+12x\)
\(\Leftrightarrow9x-3x-12x=10-6-1\)
\(\Leftrightarrow-6x=3\)
\(\Leftrightarrow x=\frac{-1}{2}\).
Vậy tập nghiệm phương trình \(S=\left\{\frac{-1}{2}\right\}\)

3) 9h30phút-30phút=9h
Gọi x(km) là quãng đường từ A đến B (ĐK X>0)
Thời gian xe đi từ A đến B là \(\dfrac{X}{15}\)(h)
Thời gian xe đi từ B đến A là \(\dfrac{X}{12}\)(h)
Theo đề bài ta có phương trình :
\(\dfrac{x}{15}+\dfrac{x}{12}=9\)
Giải pt:\(\dfrac{X}{15}+\dfrac{x}{12}=9\Leftrightarrow\dfrac{4x}{60}+\dfrac{5x}{60}=\dfrac{540}{60}\Rightarrow4x+5x=540\Leftrightarrow9x=540\Leftrightarrow x=60\)
Vậy quãng đường từ A đến B là 60 km
\(15x-3\left(3x-2\right)=45-5\left(2x-5\right)\Leftrightarrow15x-9x+6=45-10x+25\Leftrightarrow16x=64\Leftrightarrow x=4\)

1)
ĐKXĐ: x\(\ne\)3
ta có :
\(\frac{x^2-6x+9}{2x-6}=\frac{\left(x-3\right)^2}{2\left(x-3\right)}=\frac{x-3}{2}\)
để biểu thức A có giá trị = 1
thì :\(\frac{x-3}{2}\)=1
=>x-3 =2
=>x=5(thoả mãn điều kiện xác định)
vậy để biểu thức A có giá trị = 1 thì x=5
1)
\(A=\frac{x^2-6x+9}{2x-6}\)
A xác định
\(\Leftrightarrow2x-6\ne0\)
\(\Leftrightarrow2x\ne6\)
\(\Leftrightarrow x\ne3\)
Để A = 1
\(\Leftrightarrow x^2-6x+9=2x-6\)
\(\Leftrightarrow x^2-6x-2x=-6-9\)
\(\Leftrightarrow x^2-8x=-15\)
\(\Leftrightarrow x=3\) (loại vì không thỏa mãn ĐKXĐ)

\(a,3x^2+2x-1\Leftrightarrow3x^2-x+3x-1\Leftrightarrow x\left(3x-1\right)+\left(3x-1\right)\Leftrightarrow\left(3x-1\right)\left(x-1\right)\)

giải luôn ko chép đề nhé
a,
<=>(3x-5)(x-1)=(3x+1)(x-2)-3(x-1)
<=>3x^2-8x+5=3x^2-5x-2-3x+3
<=>3x^2-8x-3x^2+5x+3x=-5+3
<=>0x=-2
vậy s=\(\varnothing\)

a: \(\Leftrightarrow20x^2-12x+15x+5< 10x\left(2x+1\right)-30\)
\(\Leftrightarrow20x^2+3x+5< 20x^2+10x-30\)
=>3x+5<10x-30
=>-7x<-35
hay x>5
b: \(\Leftrightarrow4\left(5x-20\right)-6\left(2x^2+x\right)>4x\left(1-3x\right)-15x\)
\(\Leftrightarrow20x-80-12x^2-6x>4x-12x^2-15x\)
=>14x-80>-11x
=>25x>80
hay x>16/5

a) 1x−3+3=x−32−x1x−3+3=x−32−x ĐKXĐ: x≠2x≠2
Khử mẫu ta được: 1+3(x−2)=−(x−3)⇔1+3x−6=−x+31+3(x−2)=−(x−3)⇔1+3x−6=−x+3
⇔3x+x=3+6−13x+x=3+6−1
⇔4x = 8
⇔x = 2.
x = 2 không thỏa ĐKXĐ.
Vậy phương trình vô nghiệm.
b) 2x−2x2x+3=4xx+3+27

1 14-3x=-2+5x
<=>-3x-5x = -2-14
<=> -8x =-16
<=> x =-16/-8=2
mấy bạn ơi...các phương trình trên nó bị lặp lại nhak....ptrinh day ni:
a)\(14-3x=-2+5x\)
b) \(3\times\left(5x+2\right)-x\times\left(5x+2\right)=0\)
c) \(\frac{2x}{3}+\frac{3x-1}{6}=4-\frac{x}{3}\)
d) \(\frac{3-x}{x-2}+\frac{x+1}{x+2}=\frac{3x}{x^2-4}\)
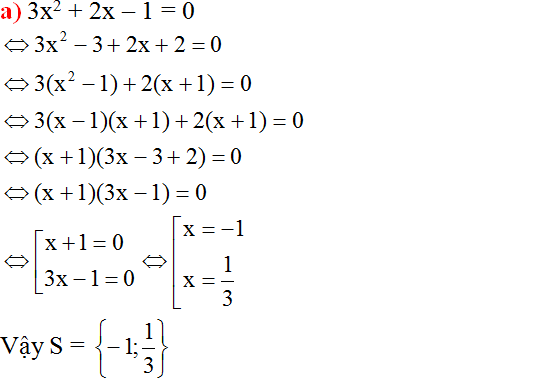
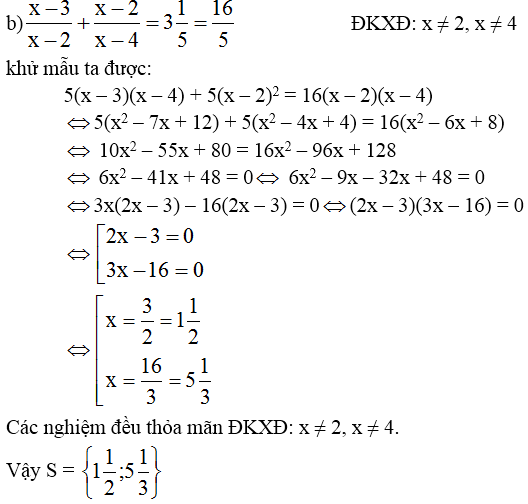
ĐK \(x\ne0\)
\(\dfrac{x^4+3x^2+1}{x^3+x^2-x}=3\)
\(\Leftrightarrow\) \(\dfrac{x^4+3x^2+1}{x^3+x^2-x}=\dfrac{3\left(x^3+x^2-x\right)}{x^3+x^2-x}\)
\(\Leftrightarrow x^4+3x^2+1=3x^3+3x^2-3x\)
\(\Leftrightarrow x^4+3x^2+1-3x^3-3x^2+3x=0\)
\(\Leftrightarrow x^4-3x^3+3x+1=0\)
Chia cả 2 vế cho \(x^2\) ta được :
\(x^2-3x+\dfrac{3}{x}+\dfrac{1}{x^2}=0\)
\(\Leftrightarrow\left(x^2+\dfrac{1}{x^2}\right)-3\left(x-\dfrac{1}{x}\right)=0\)
\(\Leftrightarrow\left(x-\dfrac{1}{x}\right)^2-2-3\left(x-\dfrac{1}{x}\right)=0\)
Đặt \(x-\dfrac{1}{x}=t\) thì phương trình trở thành :
\(t^2-3t-2=0\)
\(\Leftrightarrow\left(t-1\right)\left(t-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t-1=0\\t-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}t=1\\t=2\end{matrix}\right.\)
Với \(t=1\) :
\(\Leftrightarrow x-\dfrac{1}{x}=1\)
\(\Leftrightarrow\) \(\dfrac{x^2}{x}-\dfrac{1}{x}=\dfrac{x}{x}\)
\(\Leftrightarrow x^2-x-1=0\)
\(\Delta=1^2+4=5>0\)
\(\Rightarrow\left[{}\begin{matrix}x_1=\dfrac{1+\sqrt{5}}{2}\\x_2=\dfrac{1-\sqrt{5}}{2}\end{matrix}\right.\)
Với \(t=2\) :
\(\Leftrightarrow x-\dfrac{1}{x}=2\)
\(\Leftrightarrow\) \(\dfrac{x^2}{x}-\dfrac{1}{x}=\dfrac{2x}{x}\)
\(\Leftrightarrow x^2-2x-1=0\)
\(\Delta=\left(-2\right)^2+4=8>0\)
\(\Rightarrow\left[{}\begin{matrix}x_3=\dfrac{2+\sqrt{8}}{2}=1+\sqrt{2}\\x_4=\dfrac{2-\sqrt{8}}{2}=1-\sqrt{2}\end{matrix}\right.\)
Vậy phương trình có 4 nghiệm :
\(\left[{}\begin{matrix}x_1=\dfrac{1+\sqrt{5}}{2}\\x_2=\dfrac{1-\sqrt{5}}{2}\\x_3=1+\sqrt{2}\\x_4=1-\sqrt{2}\end{matrix}\right.\)