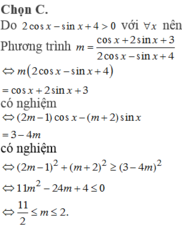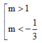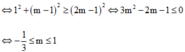K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HP
13 tháng 8 2021
1.
a, Phương trình có nghiệm khi:
\(\left(m+2\right)^2+m^2\ge4\)
\(\Leftrightarrow m^2+4m+4+m^2\ge4\)
\(\Leftrightarrow2m^2+4m\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}m\ge0\\m\le-2\end{matrix}\right.\)
b, Phương trình có nghiệm khi:
\(m^2+\left(m-1\right)^2\ge\left(2m+1\right)^2\)
\(\Leftrightarrow2m^2+6m\le0\)
\(\Leftrightarrow-3\le m\le0\)
HP
13 tháng 8 2021
2.
a, Phương trình vô nghiệm khi:
\(\left(2m-1\right)^2+\left(m-1\right)^2< \left(m-3\right)^2\)
\(\Leftrightarrow4m^2-4m+1+m^2-2m+1< m^2-6m+9\)
\(\Leftrightarrow4m^2-7< 0\)
\(\Leftrightarrow-\dfrac{\sqrt{7}}{2}< m< \dfrac{\sqrt{7}}{2}\)
b, \(2sinx+cosx=m\left(sinx-2cosx+3\right)\)
\(\Leftrightarrow\left(m-2\right)sinx-\left(2m+1\right)cosx=-3m\)
Phương trình vô nghiệm khi:
\(\left(m-2\right)^2+\left(2m+1\right)^2< 9m^2\)
\(\Leftrightarrow m^2-4m+4+4m^2+4m+1< 9m^2\)
\(\Leftrightarrow m^2-1>0\)
\(\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -1\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 9 2020
c/
\(\Leftrightarrow\frac{1}{2}sin2x-\frac{\sqrt{3}}{2}cos2x=\frac{\sqrt{3}}{2}sinx+\frac{1}{2}cosx\)
\(\Leftrightarrow sin\left(2x-\frac{\pi}{3}\right)=sin\left(x+\frac{\pi}{6}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\frac{\pi}{3}=x+\frac{\pi}{6}+k2\pi\\2x-\frac{\pi}{3}=\frac{5\pi}{6}-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k2\pi\\x=\frac{7\pi}{18}+\frac{k2\pi}{3}\end{matrix}\right.\)
2.
Theo điều kiện có nghiệm của pt lượng giác bậc nhất với sin và cos:
\(m^2+\left(m-1\right)^2\ge5\)
\(\Leftrightarrow m^2-m-2\ge0\Leftrightarrow\left[{}\begin{matrix}m\ge2\\m\le-1\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 9 2020
a/
\(\Leftrightarrow\sqrt{2}sin\left(x-\frac{\pi}{4}\right)=\sqrt{3}\)
\(\Leftrightarrow sin\left(x-\frac{\pi}{4}\right)=\sqrt{\frac{3}{2}}>1\)
Pt vô nghiệm
b/
\(\Leftrightarrow\frac{2}{\sqrt{13}}sinx+\frac{3}{\sqrt{13}}cosx=\frac{2}{\sqrt{13}}\)
Đặt \(\frac{2}{\sqrt{13}}=cosa\) với \(a\in\left(0;\pi\right)\)
\(\Rightarrow sinx.cosa+cosx.sina=cosa\)
\(\Leftrightarrow sin\left(x+a\right)=sin\left(\frac{\pi}{2}-a\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x+a=\frac{\pi}{2}-a+k2\pi\\x+a=\frac{\pi}{2}+a+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}-2a+k2\pi\\x=\frac{\pi}{2}+k2\pi\end{matrix}\right.\)
V
1
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 11 2021
\(\Rightarrow sinx+2=m.cosx\)
\(\Rightarrow sinx-m.cosx=-2\)
Pt đã cho vô nghiệm khi:
\(1^2+\left(-m\right)^2< \left(-2\right)^2\)
\(\Rightarrow m^2< 3\)
\(\Rightarrow-\sqrt{3}< m< \sqrt{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 10 2020
a/
\(\left(m+1\right)^2+\left(m-1\right)^2\ge\left(2m+3\right)^2\)
\(\Leftrightarrow2m^2+12m+7\le0\)
\(\Leftrightarrow\frac{-6-\sqrt{22}}{2}\le m\le\frac{-6+\sqrt{22}}{2}\)
b/ \(\Leftrightarrow\left\{{}\begin{matrix}m\ge0\\\left(m-1\right)^2+4m\ge m^4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ge0\\m^4-\left(m+1\right)^2\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ge0\\\left(m^2+m+1\right)\left(m^2-m-1\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow0\le m\le\frac{1+\sqrt{5}}{2}\)
c/ \(\Leftrightarrow\frac{1}{2}sin2x-\frac{\sqrt{3}}{2}cos2x+\frac{1}{2}=m\)
\(\Leftrightarrow sin\left(2x-\frac{\pi}{3}\right)+\frac{1}{2}=m\)
Do \(-\frac{1}{2}\le sin\left(2x-\frac{\pi}{3}\right)\le\frac{3}{2}\Rightarrow-\frac{1}{2}\le m\le\frac{3}{2}\)
CM
13 tháng 6 2019
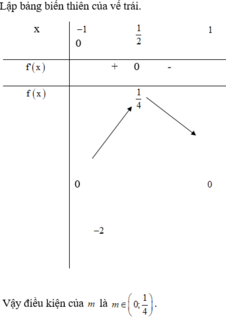
Hướng dẫn giải:
Chọn A.
Ta có: sin2x – 2( m- 1)sinx. cosx – (m- 1).cos2x = m
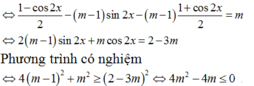
