Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔANH và ΔAHC có:
∠(NAH) chung
∠(ANH) = ∠(AHN) = 90o
⇒ ΔANH ∼ ΔAHC (g.g)
b) Ta có :
![]()
![]()
Tương tự : CH = 5 (cm)
⇒ BC = BH + CH = 9 + 5 = 14 (cm)
c) Theo chứng minh trên ta có:
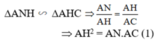
Chứng minh tương tự ta có :
ΔAMH ∼ ΔAHB ⇒ AH2 = AM.AB (2)
Từ (1) và (2) ⇒ AN.AC = AM.AB (3)
Xét ΔAMN và ΔACB có :
∠A chung
AN.AC = AM.AB
⇒ ΔAMN ∼ ΔACB (c.g.c)
d) Ta có : ΔAMH ∼ ΔAHB
![]()
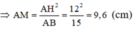
Lại có ΔAMN ∼ ΔACB (cmt)
![]()
![]()

a. xét tam giác ABC và tam giác HAC có
góc ACB= góc HCA ( góc chung)
góc BAC = góc AHC (=90độ)
do đó tam giác ABC đồng dạng với tam giác HAC(g.g)
b. theo bài ra ta có góc BAC=90 độ
suy ra tam giác ABC vuôg tại A
ta lại có AB=6cm, AC=8cm
suy ra AB ^2+ AC^2= BC^2
thay vào ta có 6^2+ 8^2= BC^2
suy ra BC^2= 10^2
suy ra BC = 10 (cm)

mình tóm tắt thôi nha
▲MHA đồng dạng ▲HBA(g-g)
▲ABC đồng dạng ▲HBA(g-g)
suy ra ▲MHA đồng dạng ▲ABC
▲MHA đồng đăng ▲ANM
suy ra ▲ANM đồng dạng ▲ABC
suy ra tỉ số rồi ra
b)áp dụng PY-ta-go thì
BC =25cm
ta có S▲ABC =1/2 AB.AC
mặt khác S▲ABC=1/2 AH.BC
suy ra AB.AC=AH.BC
suy ra AH=(15.20)/25=12cm
ta có ▲ANM đồng dạng ▲ABC
suy ra \(\frac{NM}{BC}=\frac{AM}{AC}\)
\(\Rightarrow\frac{AH}{BC}=\frac{AM}{AC}=\frac{12}{25}\)
\(\Rightarrow\frac{S▲ANM}{S▲ABC}=\left(\frac{12}{25}\right)^2=0,2304\)
nhớ kick cho mình nha
câu b) tính tỉ số diện tích dùm mình lun nha bạn cần gắp lắm!!!!!!!!!!
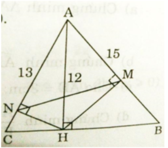
A ) ÁP DỤNG ĐỊNH LÍ PITAGO TA CÓ :
\(BH^2=AB^2-AH^2\)
\(\Leftrightarrow\)\(15^2-12^2=81\)
\(\Rightarrow BH=\sqrt{81}=9\)(cm)
Ap dụng pitago ta lại có :
\(HC^2=AC^2-AH^2\)
\(\Leftrightarrow HC^2=13^2-12^2=25\left(CM\right)\)
\(\Rightarrow HC=\sqrt{25}=5\left(cm\right)\)
Vậy : \(BC=BH+HC=5+9=14\left(cm\right)\)
sao lại sử dụng Py - ta - go đc ? tam giác ABC nhọn mà