Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

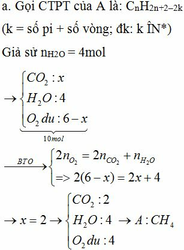
pt:
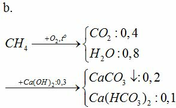
CO2 + Ca(OH)2 → CaCO3↓ + H2O
0,3 → 0,3 0,3
CO2 + CaCO3 + H2O → Ca(HCO3)2
0,1 → 0,1 0,1
m dd tăng = mCO2 + mH2O – mCaCO3 = 12g

nO2= 0,2 mol.
m O2= 6,4 gam
=> tổng m H2O + CO2= 1,6 + 6,4= 8 gam .
gọi a là nCO2 => 2a là nH2O. ta có :
44a + 36a= 8 => a= 0,1 mol
=> mCO2= 4,4 gam
=>mH2O= 3,6 gam
b. nCO2= 0,1 mol => nC= 0,1 mol
nH2O= 0.2 mol => nH= 0,4 mol
nC:nH= 1:4 =>CTPT có dạng (CH4)n.
vì M_Y= 16 <=> 16n=>n=1. => CTPT của Y là CH4.

Y gồm \(\left\{{}\begin{matrix}A:a\left(mol\right)\\CO_2:b\left(mol\right)\\H_2O:c\left(mol\right)\end{matrix}\right.\)
Z gồm \(\left\{{}\begin{matrix}A:a\left(mol\right)\\CO_2:b\left(mol\right)\end{matrix}\right.\)
Do nZ = 50%.nY
=> a + b = 0,5a + 0,5b + 0,5c
=> \(c=a+b\)
Khí thoát ra khỏi dd NaOH là khí A
\(n_{CO_2}=83,33\%.n_Z\)
=> b = 0,8333.(a + b)
=> 5a = b
=> Y gồm \(\left\{{}\begin{matrix}A:a\left(mol\right)\\CO_2:5a\left(mol\right)\\H_2O:6a\left(mol\right)\end{matrix}\right.\)
=> nC(A pư) : nH(A pư) = 5a : 12a = 5 : 12
=> CTPT: (C5H12)n
Chọn n = 1 thỏa mãn => CTPT: C5H12

a, \(CH_4+2O_2\underrightarrow{t^o}CO_2+2H_2O\)
\(2C_2H_2+5O_2\underrightarrow{t^o}4CO_2+2H_2O\)
Ta có: \(n_{CH_4}+n_{C_2H_2}=\dfrac{6,72}{22,4}=0,3\left(mol\right)\left(1\right)\)
\(n_{CO_2}=n_{CH_4}+2n_{C_2H_2}=\dfrac{7,84}{22,4}=0,35\left(mol\right)\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}n_{CH_4}=0,25\left(mol\right)\\n_{C_2H_2}=0,05\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\%V_{CH_4}=\dfrac{0,25.22,4}{6,72}.100\%\approx83,33\%\\\%V_{C_2H_2}\approx16,67\%\end{matrix}\right.\)
Theo PT: \(n_{O_2}=2n_{CH_4}+\dfrac{5}{2}n_{C_2H_2}=0,625\left(mol\right)\Rightarrow m_{O_2}=0,625.32=20\left(g\right)\)
nhưng giữ kiện đè bài cho có cái 40% đâu