Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi số cần tìm là a ta có
\(\frac{2+a}{11+a}\)=\(\frac{6}{7}\)
=>7x(2+a)=6x(11+a)
14+7xa=66+6xa
7xa+6xa=66-14
13xa=52
a=52:13
a=4
Gọi a là số tự nhiên cộng thêm vào tử và mẫu số
Ta có:
\(\frac{2+a}{11+a}=\frac{6}{7}\)
\(\Rightarrow7\left(2+a\right)=6\left(11+a\right)\)
\(14+7a=66+6a\)
\(7a-6a=66-14\)
\(\Rightarrow a=52\)
Vậy, số tự nhiên cần tìm là 52

Hiệu của mẫu số và tử số của phân số 2 11 là: 11 – 2 = 9
Khi cộng thêm vào mẫu số và tử số của phân số 2 11 với cùng một số thì ta được phân số mới có hiệu của mẫu số và tử số vẫn bằng 9.
Vì phân số mới rút gọn thì bằng 6 7 nên ta có:
Tử số:
|
|
|
|
|
|
|
|
|
|
|
|
Mẫu số : 9
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Hiệu số phần bằng nhau: 7 – 6 = 1 (phần)
Tử của phân số mới là: 9 x 6 = 54
Mẫu của phân số mới là 9 x 7 = 63
Phân số mới là 54 63
Số tự nhiên phải tìm là 54 – 2 = 52 ( hoặc 63 – 11 = 52)
Vậy số phải tìm là 52


Hiệu số phần bằng nhau: 7 – 6 = 1 (phần)
Tử của phân số mới là: 9 x 6 = 54
Mẫu của phân số mới là 9 x 7 = 63
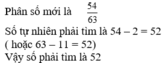

Khi cộng thêm cả tử và mẫu số với cùng một số thì hiệu của hai số không thay đổi
Hiệu hai số ban đầu là 19 - 7 = 12
Phân số mới bằng 4/6
Coi tử số mới là 4 phần, mẫu số mới là 6 phần
Hiệu số phần bằng nhau là: 6 - 4 = 2 phần
Tử số mới là: 12 : 2 x 4 = 24
Vậy số cần cộng thêm là: 24 - 7 = 17
ĐS: 17
bài giải
hiệu số phần bằng nhau là:
6 - 4 = 2 phần
tử số mới là:
12 : 2 x 4 = 24
số cần cộng thêm là:
24 - 7 = 17
Đáp số:..............
hok tốt

111111111111111111111111111111111111111111111111111111111111
Hiệu của tử số và mẫu số ban đầu là:
19 - 7 = 12
Vì cùng cộng thêm vào tử số và mẫu số cùng một số tự nhiên nên hiệu không thay đổi
Coi tử số mới là 4 phần bằng nhau, mẫu số mới là 6 phần như thế.
Tử số mới là:
12 : (6 - 4) x 4 = 24
Số tự nhiên cần tìm là:
24 - 7 = 17
Đáp số: 17


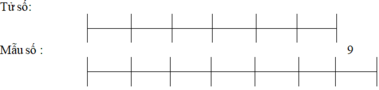

Hiệu tử số và mẫu số :
`11-2=9`
Hiệu số phần bằng nhau :
`7-6=1(phần)`
Tử số mới :
`9:1xx6=54`
Số cần tìm :
`54 - 2 = 52`
Vậy số cần tìm là : `52`
\(\dfrac{2}{11}=\dfrac{2+16}{11+10}=\dfrac{18}{21}=\dfrac{6}{7}\)