
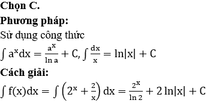
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

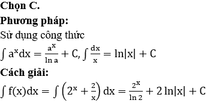

Biến đổi :
\(4\sin x+3\cos x=A\left(\sin x+2\cos x\right)+B\left(\cos x-2\sin x\right)=\left(A-2B\right)\sin x+\left(2A+B\right)\cos x\)
Đồng nhất hệ số hai tử số, ta có :
\(\begin{cases}A-2B=4\\2A+B=3\end{cases}\)\(\Leftrightarrow\begin{cases}A=2\\B=-1\end{cases}\)
Khi đó \(f\left(x\right)=\frac{2\left(\left(\sin x+2\cos x\right)\right)-\left(\left(\sin x-2\cos x\right)\right)}{\left(\sin x+2\cos x\right)}=2-\frac{\cos x-2\sin x}{\sin x+2\cos x}\)
Do đó,
\(F\left(x\right)=\int f\left(x\right)dx=\int\left(2-\frac{\cos x-2\sin x}{\sin x+2\cos x}\right)dx=2\int dx-\int\frac{\left(\cos x-2\sin x\right)dx}{\sin x+2\cos x}=2x-\ln\left|\sin x+2\cos x\right|+C\)

ta có:
\(y'=\frac{\left(\frac{1-x^2}{1+x^2}\right)'}{\frac{1-x^2}{1+x^2}}=\frac{\frac{-2x.\left(1+x^2\right)-2x.\left(1-x^2\right)}{\left(1+x^2\right)^2}}{\frac{1-x^2}{1+x^2}}=\frac{\frac{-4x}{\left(1+x^2\right)^2}}{\frac{1-x^2}{1+x^2}}=\frac{-4x}{\left(1+x^2\right)\left(1-x^2\right)}=\frac{-4x}{1-x^4}\)

Từ \(f\left(x\right)+f\left(\frac{1}{x}\right)=x^2\); lần lượt thay \(x=2\) và \(x=\frac{1}{2}\) vào, ta có:
\(f\left(2\right)+3f\left(\frac{1}{2}\right)=4\) và \(f\left(\frac{1}{2}\right)+3f\left(2\right)=\frac{1}{4}\Leftrightarrow3f\left(2\right)+f\left(\frac{1}{2}\right)=\frac{1}{4}\)
Giải hệ phương trình với 2 ẩn \(f\left(2\right)\) và \(f\left(\frac{1}{2}\right)\)
Tìm được \(f\left(2\right)=\frac{-13}{32}\)
Ta có \(f\left(x\right)+3f\left(\frac{1}{x}\right)=x^2\) (1)
Thay \(x\rightarrow\frac{1}{x}\) được \(f\left(\frac{1}{x}\right)+3f\left(x\right)=\frac{1}{x^2}\)
\(\Leftrightarrow3f\left(\frac{1}{x}\right)+9f\left(x\right)=\frac{3}{x^2}\) (2)
Lấy (2) trừ (1) theo vế : \(8f\left(x\right)=\frac{3}{x^2}-x^2\)
\(\Leftrightarrow f\left(x\right)=\frac{1}{8}\left(\frac{3}{x^2}-x^2\right)\)
Vậy f(2) = -13/32

ta có:
\(y'=\frac{\left(x+\sqrt{x^2+1}\right)'}{x+\sqrt{x^2+1}}=\frac{1+\frac{x}{\sqrt{x^2+1}}}{x+\sqrt{x^2+1}}=\frac{1+\frac{x}{\sqrt{x^2+1}}}{x+\sqrt{x^2+1}}=\frac{\frac{x+\sqrt{x^2+1}}{\sqrt{x^2+1}}}{x+\sqrt{x^2+1}}=\frac{1}{\sqrt{x^2+1}}\)
Mình đang cần giải gấp
Tìm nguyên hàm hàm số sau :
\(\left(\frac{2}{\sqrt{x}}+3^x-tanx+3x-2\right)dx\)

bạn làm thế này nhé
= \(\left(a\sqrt{x}+\frac{3^x}{ln3^2}+lncosx+\frac{3}{2}x^2-2x+C\right)\)