Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
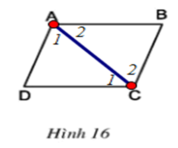
Hình thang ABCD có đáy AB, CD ⇒ AB // CD ⇒ ∠A2 = ∠C1 ̂ (hai góc so le trong)
Lại có: AD // BC ⇒ ∠A1 = ∠C2 (hai góc so le trong)
Xét ΔABC và ΔCDA có:
∠A2 = ∠C1 (cmt)
AC chung
∠A1 = ∠C2 (cmt)
⇒ ΔABC = ΔCDA (g.c.g)
⇒ AD = BC, AB = CD (các cặp cạnh tương ứng)
b)
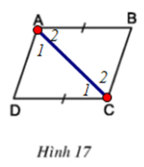
Xét ΔABC và ΔCDA có:
AC chung
∠A2 = ∠C1 (cmt)
AB = CD
⇒ ΔABC = ΔCDA (c.g.c)
⇒ AD = BC (hai cạnh tương ứng)
∠A1 = ∠C2 (hai góc tương ứng) ⇒ AD // BC (hai góc so le trong bằng nhau)
tự vẽ hình
a) Xét tam giác DAC và tam giác BCA có:
góc DAC = góc BCA (slt do AD // BC)
AC: chung
góc DCA = góc BAC (slt do AB // DC)
suy ra: tam giác DAC = tam giác BCA (g.c.g)
=> AD = BC; DC = AB
b) Xét tam giác DAC và tam giác BCA có:
AD = AB
góc DCA = góc BAC (slt do AB // CD)
AC: chung
suy ra: tam giác DAC = tam giác BCA (c.g.c)
=> AD = BC
góc DAC = góc BCA
mà 2 góc này slt
=> AD // BC
a) Ta có : AB // CD ( do ABCD là hình thang )
AD // BC ( gt )
=> ABCD là hình bình hành
=> AD = BC ; AB = CD
b) Ta có : AB = CD ( gt )
AB // CD ( gt )
=> ABCD là hình bình hành
=> AD // BC ; AD = BC
- Hình bạn tự vẽ nhé!
- Kéo dài AD và BC cắt nhau tại E
- Vì ABCD là hình thang
=> AB // DC
=> góc EAB = góc EDC
góc EBA = góc ECD
( các góc đồng vị)
mà góc EDC = góc ECD (gt)
=> góc EAB = góc EBA (bắc cầu)
=> tam giác EAB cân tại E
tam giác EDC cân tại E
=> EA = EB
ED = EC
=> ED - EA = EC - EB (bắc cầu)
=> AD = BC (đpcm)
Chúc bạn học tốt <3
Xét hình thang ABCD có \(\widehat{ADC}=\widehat{BCD}\)
nên ABCD là hình thang cân
Suy ra: AD=BC
Bài 2:
Xét ΔBAC có BA=BC
nên ΔBAC cân tại B
Suy ra: \(\widehat{BAC}=\widehat{BCA}\)
mà \(\widehat{BAC}=\widehat{ACD}\)
nên \(\widehat{ACB}=\widehat{ACD}\)
hay CA là tia phân giác của \(\widehat{BCD}\)
Bài 7. Cho hình thang ABCD, đáy AB = 40cm, CD = 80cm, BC = 50cm, AD = 30cm. Chứng minh rằng ABCD là hình thang vuông.
Từ A kẻ AG // BC cắt CD tại G
Ta có: Hình thang ABCD (giả thiết)
⇒ AB // CD
⇒ AB // GC (vì G ∈ CD)
Xét tứ giác ABCG, có:
AB // GC (chứng minh trên)
AG // BC (giả thiết)
⇒ Tứ giác ABCG là hình bình hành
⇒ AB = GC = 40 cm
AG = BC = 50 cm
Ta có: DG = CD - GC (vì G ∈ CD)
⇒ DG = 80 - 40
⇒ DG = 40(cm)
Xét Δ AGD, có:
AG2=AD2+DG2
=> 502= 30^2 +40^2
=> 50^2 = 2500
=> 50^2 = 50^2
⇒ ΔAGD vuông tại D
⇒ Hình thang ABCD là hình thang vuông
Từ A kẻ AG // BC cắt CD tại G
Ta có: Hình thang ABCD (giả thiết)
⇒ AB // CD
⇒ AB // GC (vì G ∈ CD)
Xét tứ giác ABCG, có:
AB // GC (chứng minh trên)
AG // BC (giả thiết)
⇒ Tứ giác ABCG là hình bình hành
⇒ AB = GC = 40 cm
AG = BC = 50 cm
Ta có: DG = CD - GC (vì G ∈ CD)
⇒ DG = 80 - 40
⇒ DG = 40(cm)
Xét Δ AGD, có:
AG2=AD2+DG2AG2=AD2+DG2
⇒502=302+402⇒502=302+402
⇒502=900+1600
⇒502=2500
⇒502=502
⇒ ΔAGD vuông tại D
⇒ Hình thang ABCD là hình thang vuông
hơi dài nha
a) Kẻ đoạn thẳng AC.
Ta có: AB // CD (ABCD là hình thang)
Xét \(\Delta ABC\) và \(\Delta DCA\), có:
\(\widehat{BAC} = \widehat{ACD}\) (hai góc so le trong, AB//CD)
AC là cạnh chung
\(\widehat{DAC} = \widehat{BCA}\) (hai góc so le trong, AD // BC)
Vậy \(\Delta ABC=\Delta CDA\) (g.c.g)
\(\Rightarrow AD=BC;AB=CD\) (ĐPCM)
b) Xét \(\Delta ADC\) và \(\Delta CBA\), có:
AB = CD (gt)
\(\widehat{BAC} = \widehat{ACD}\) ((hai góc so le trong, AB//CD)
AC là cạnh chung
\(\Rightarrow\Delta ADC=\Delta CBA\) (c.g.c)
\(\Rightarrow\) \(\widehat{DAC} = \widehat{BCA}\) (hai góc tương ứng), mà 2 góc này ở vị trí so le trong
\(\Rightarrow\) AD // BC
Ta có: \(\Delta ADC=\Delta CBA\) \(\Rightarrow\) AD = BC (hai cạnh tương ứng)
Vậy AD // BC, AD = BC (đpcm)
Từ A kẻ AE//BC cắt CD tại E => ABCE là hình bình hành => EC = AB = 40cm
và AE = BC = 50cm , DE = DC - EC = 80 - 40 = 40cm
xét tam giác ADE có AE^2=2500, DE^2 = 1600, DA^2 = 900
=> AE^2= DE^2 + DA^2 => tam giác ADE vuông tại D
thang ABCD có cạnh bên AD vuông góc đáy CD => thang vuông
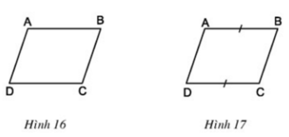
Xét ΔADC và ΔCBA, có:
AB = CD (gt)
^ BAC = ^ ACD (hai góc so le trong)
AC là cạnh chung
⇒ ΔADC = ΔCBA (c.g.c)
⇒ ^ DAC = ^ BCA (hai góc tương ứng), mà 2 góc này ở vị trí so le trong
⇒ AD // BC
Ta có: ΔADC = ΔCBA
⇒ AD = BC (hai cạnh tương ứng)
Vậy AD // BC, AD = BC (đpcm
Thanks bạn nha <3