Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(dt\left(ABCD\right)=\dfrac{AB+CD}{2}.DE=\dfrac{10+6}{2}.5=40\left(cm^2\right)\)
b) Xem hình vẽ
A B C D E 6 4 5 F
Tam giác vuông EAD có: \(AE=\sqrt{AD^2-DE^2}=\sqrt{5^2-4^2}=3\)
Vì ABCD là hình thang cân nên AE = FB = 3.
Suy ra AB = EF + AE + FB = 6 + 3 + 3 = 12.
\(dt\left(ABCD\right)=\dfrac{AB+CD}{2}.DE=\dfrac{12+6}{2}.4=36\left(cm^2\right)\)

ta có tam giác ADH vuông tại H
=> AH^2+HD^2=AD^2
=>HD^2=AD^2-AH^2
=5^2-4^2
=9
=>HD=3 cm
kẻ BK vuông góc với CD
=>ABKH là hình chữ nhật
=>AH=BK=4cm
tam giác BKC vuông tại K
=>BK^2+KC^2=BC^2
=>KC^2=BC^2-BK^2
=80-16
=64
=>KC=8 (cm)
lại có DH+HK+KC=20
=>HK=20-3-8=9 (cm)
=>AB+HK=9 cm
ta có chu vi hình thang ABCD là AB+BC+CD+DA=9+√80+20+5=34+√80(cm)

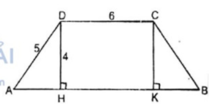
Xét hình thang cân ABCD có AB // CD
Đáy nhỏ CD = 6cm, cạnh bên AD = 5cm
Đường cao DH = 4cm. Kẻ CK ⊥ AB
Ta có tứ giác CDHK là hình chữ nhật
HK = CD = 6cm
△ AHD vuông tại H. Theo định lý Pi-ta-go ta có: A D 2 = A H 2 + D H 2
⇒ A H 2 = A D 2 - D H 2 = 5 2 - 4 2 = 25 – 16 = 9 ⇒ AH = 3cm
Xét hai tam giác vuông DHA và CKB :
∠ (DHA)= ∠ (CKB)= 90 0
AD = BC (tính chất hình thang cân)
∠ A = ∠ B(gt)
Do đó: △ DHA = △ CKB (cạnh huyền, góc nhọn)
⇒ KB = AH = 3 (cm)
AB = AH + HK + KB = 3 + 6 + 3 = 12 (cm)
S A B C D = (AB + CD) / 2. DH = (12 + 6) / 2. 4 = 36( c m 2 )

Ta có: h £ AD = 4cm
Þ maxS = 4.10 :2 =20cm2