
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn B
Giả sử số đỉnh của đa giác đáy của lăng trụ là n
Khi đó số cạnh của 2 mặt đáy là 2n và số cạnh bên của lăng trụ là n
Vậy số cạnh của lăng trụ là 3n. Ta thấy 3.673 = 2019 nên chọn đáp án B.

Chọn D.
Nhận xét: Số đỉnh của đa giác đáy lăng trụ bằng số cạnh của đa giác đáy lăng trụ và cũng bằng số cạnh bên của lăng trụ. Do hình lăng trụ có 2 đáy nên số cạnh của hình lăng trụ chắc chắn là một số chia hết cho 3. Trong 4 đáp án chỉ có 2019 là số chia hết cho 3.

Đáp án B.
Số cạnh của hình lăng trụ là 3n luôn chia hết cho 3.
Chỉ có đáp án B thỏa mãn.

Chọn A.
Hình lăng trụ có đáy là đa giác n cạnh thì sẽ có số cạnh là 3n. Vậy số cạnh của hình lăng trụ phải là một số chia hết cho 3.

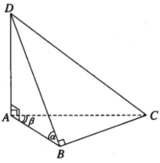
Tứ diện ABCD có ∠ BAD = 90 ° nên ∠ ABD = α là một góc nhọn. Khi quay các cạnh của tứ diện đó xung quanh cạnh AB thì cạnh BD tạo thành một hình nón tròn xoay đỉnh B có trục là AB, cạnh AD vuông góc với AB tạo thành đáy của hình nón đó.
Mặt khác theo giả thiết ta có BD ⊥ BC nên AB ⊥ BC. Ta có ∠ BAC = β là một góc nhọn. Do đó khi quay các cạnh của tứ diện xung quanh cạnh AB thì cạnh AC tạo thành một hình nón tròn xoay đỉnh A có trục là AB, còn cạnh BC tạo thành đáy của hình nón.
Như vậy khi quay tất cả các cạnh của tứ diện xung quanh trục AB thì các cạnh BD và AC tạo thành hai hình nón.

Đáp án A
Vì số cạnh của hình lăng trụ phải là một số chia hết cho 3, trong các đáp án chỉ có 2019 chia hết cho 3.

Đáp án D.
Phương pháp giải: Dựng hình, dựa vào tam giác cân để xác định các yếu tố vuông góc
Lời giải: Với hình chóp tam giác đều S.ABC thì: góc giữa các cạnh bên và mặt đáy bằng nhau, hình chiếu vuông góc của S trên mặt phẳng (ABC) là trọng tâm tam giác ABC, hai cạnh đối diện vuông góc với nhau.

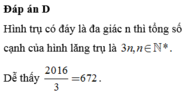
Đa giác 17 cạnh có 17 cạnh .