Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là B
Ta có: S H ⊥ A B ⇒ S H ⊥ A B C D .
Do A B / / C D ⇒ S A B ∩ S C D = S x / / A B . Mặt khác S H ⊥ C D S K ⊥ C D ⇒ S H ⊥ S x S K ⊥ S x
Suy ra góc giữa hai mặt phẳng S A B và S C D là góc giữa hai đường thẳng S H và S K .
Ta có: S H = 3 a 2 , H K = a . .
Xét tam giác S H K : tan H S K ^ = H K S H = 2 a a 3 = 2 3 3 .
Vậy tan α = 2 3 3 .
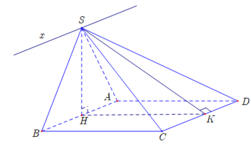

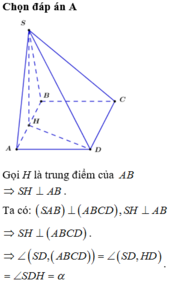
Đáp án A
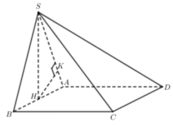
Gọi H là trung điểm của AB .
Lại có: S A B ⊥ A B C D ⇒ S H ⊥ A B C D .
Do A D / / B C nên giao tuyến d của (SAD) và (SBC) đi qua S và song song với AD.
Do A D ⊥ A B A D ⊥ S H ⇒ A D ⊥ S A B ⇒ d ⊥ S A B .Suy ra góc giữa hai mặt phẳng (SAD) và (SBC) bằng 180 ∘ − AS B ⏜ = 60 ∘ .

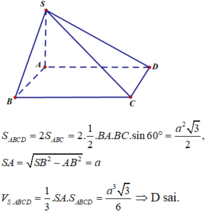


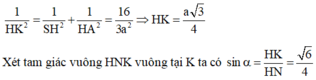



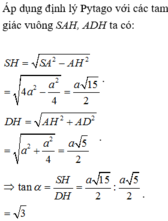
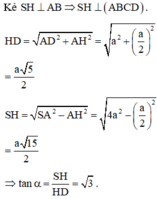
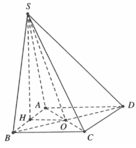
Đáp án D
Sử dụng mối quan hệ vuông góc giữa đường thẳng với đường thẳng, đường thẳng với mặt phẳng.
- Hai mặt phẳng cùng vuông góc với đường thẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng đó.
- Một đường thẳng vuông góc với hai đường thẳng cắt nhau thì nó vuông góc với mặt phẳng chứa hai đường thẳng đó.
- Một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.
Vì S A B ⊥ A B C D S A D ⊥ A B C D S A B ∩ S A D = S A ⇒ S A ⊥ A B C D ⇒ S A ⊥ B C
Mà A H ⊥ S B nên A H ⊥ S B C ⇒ A H ⊥ S C .
Tương tự ta có A K ⊥ S C D ⇒ A H ⊥ S C .
Do đó S C ⊥ A H K ⇒ S C ⊥ H K ⇒ A đúng.
S A ⊥ A B C D ⇒ S A ⊥ A C ⇒ B đúng.
B C ⊥ A H c m t ⇒ C đúng.