Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
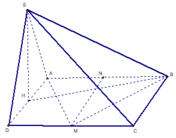
Gọi H là trung điểm của AD, N là trung điểm của AB
Có S H ⊥ A B C D ⇒ góc giữa SB và A B C D là góc SBH
Có
H B = a 2 + a 2 2 = a 5 2 S H = H B . tan S B H = a 5 2 . tan 60 0 = a 15 2 . S Δ M A B = 1 2 . M N . A B = a 2 2 V S . M A B = 1 3 . S H . S Δ M A B = 1 3 . a 15 2 . a 2 2 = a 3 15 12

Chọn đáp án C.
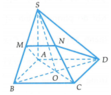
Gọi O là tâm của hình vuông ABCD thì B D ⊥ S A O

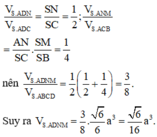


Đáp án A
Phương pháp: Xác định góc giữa hai mặt phẳng bằng cách xác định góc giữa hai đường thẳng lần lượt vuông góc với giao tuyến.
Cách giải:
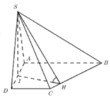
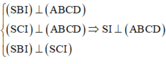
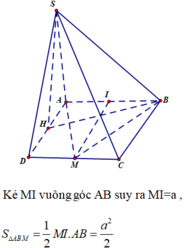
Kẻ IH
⊥
CD ta có: 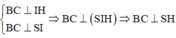
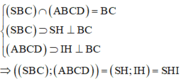
Ta có: 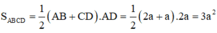
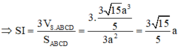
Gọi E là trung điểm của AB => EC = AD = 2a
![]()
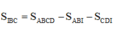
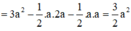
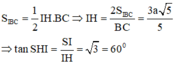


Đáp án C
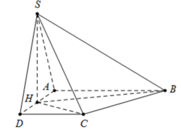
Tam giác SAD đều cạnh 2 a ⇒ S H = a 3 ⇒ H C − 2 a 3 .
Kẻ BK vuông góc H C ⇒ B K ⊥ S H C ⇒ B K − 2 a 6
Diện tích tam giác BHC là S Δ B H C = 1 2 B K . H C = 6 a 2 2
Mà S A B C D = S Δ H A B + S Δ H C D + S Δ H B C = 1 2 S A B C D + S Δ H B C ⇒ S A B C D = 2 x S Δ H B C = 12 a 2 2
V S . A B C D = 1 3 . S H . S Δ H B C = 1 3 . a 3 .12 a 2 2 = 4 6 a 3



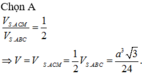

Đáp án D
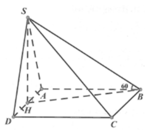
Gọi H là trung điểm của AD, N là trung điểm của AB
Có S H ⊥ A B C D ⇒ góc giữa SB và (ABCD) là góc SBH
Có
H B = a 2 + a 2 2 = a 5 2 S H = H B . tan S B H = a 5 2 . tan 60 0 = a 15 2 . S Δ M A B = 1 2 . M N . A B = a 2 2 V S . M A B = 1 3 . S H . S Δ M A B = 1 3 . a 15 2 . a 2 2 = a 3 15 12