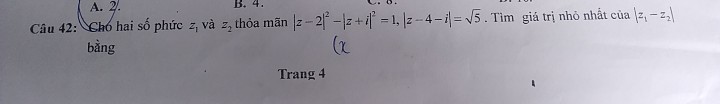K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MA
0
HN
25 tháng 10 2021
a. Để hàm số đã cho có một cực trị thì -m(2m-1)>0 \(\Rightarrow\) 0<m<1/2.
b. Để hàm số đã cho có ba cực trị thì -m(2m-1)<0 \(\Rightarrow\) m<0 hoặc m>1/2.
c. Để hàm số đã cho có một cực trị là cực đại thì m<0 và -(2m-1)<0, suy ra không có giá trị nào của m thỏa yêu cầu của bài toán.
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 1 2022
Mặt cầu tâm \(I\left(1;1;0\right)\) bán kính \(R=5\)
\(\Rightarrow IA=\sqrt{6^2+8^2}=10=2R\)
Gọi C là trung điểm IA \(\Rightarrow C\left(4;5;0\right)\Rightarrow IC=R=5\Rightarrow C\in\left(S\right)\)
Gọi D là trung điểm IC \(\Rightarrow D\left(\dfrac{5}{2};3;0\right)\), đồng thời do D là trung điểm IC \(\Rightarrow MD\perp IC\) và IM=IC=R hay tam giác MDF vuông tại D
Lại có: \(CM=CA=CI=R\Rightarrow\) tam giác AMI vuông tại M
\(\Rightarrow\Delta_VMID\sim\Delta_VAIM\) (chung góc I)
\(\Rightarrow\dfrac{MA}{MD}=\dfrac{AI}{AM}=\dfrac{2R}{R}=2\Rightarrow MA=2MD\)
\(\Rightarrow P=MA+2MB=2MD+2MB=2\left(MD+MB\right)\ge2DB=2\sqrt{\left(\dfrac{5}{2}\right)^2+\left(3-8\right)^2+0^2}=5\sqrt{5}\)
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 6 2021
Không ai vẽ hình khi làm bài mặt cầu Oxyz đâu bạn, chỉ cần đại số hóa nó là được.
Gọi I là tâm mặt cầu, do mặt cầu tiếp xúc (Q) tại H nên \(IH\perp\left(Q\right)\)
\(\Rightarrow\) Đường thẳng IH nhận vtpt của (Q) là 1 vtcp
\(\Rightarrow\) IH nhận (1;1;-1) là 1 vtcp
Phương trình IH: \(\left\{{}\begin{matrix}x=1+t\\y=-1+t\\z=-t\end{matrix}\right.\)
I vừa thuộc IH vừa thuộc (P) nên là giao điểm của IH và (P)
\(\Rightarrow\) Tọa độ I thỏa mãn:
\(2\left(1+t\right)+\left(-1+t\right)+\left(-t\right)-3=0\)
\(\Rightarrow t=1\Rightarrow I\left(2;0;-1\right)\)
\(\Rightarrow\overrightarrow{IH}=\left(-1;-1;1\right)\Rightarrow R=IH=\sqrt{3}\)
Phương trình (S):
\(\left(x-2\right)^2+y^2+\left(z+1\right)^2=3\)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 4 2021
Gọi \(M\left(x;y\right)\) là điểm biểu diễn z trên mặt phẳng tọa độ
Gọi \(A\left(-2;1\right)\) ; \(B\left(2;3\right)\) ; \(C\left(-1;2\right)\)
\(\Rightarrow\overrightarrow{AB}=\left(4;2\right)\Rightarrow AB=2\sqrt{5}\)
Từ \(\left|z+2-i\right|+\left|z-2-3i\right|=2\sqrt{5}\Leftrightarrow MA+MB=2\sqrt{5}\)
\(\Leftrightarrow MA+MB=AB\Leftrightarrow\) M nằm trên đoạn thẳng AB
\(\left|z+i-2i\right|=MC\) đạt GTNN khi và chỉ khi M là hình chiếu vuông góc của C lên AB
Phương trình đường thẳng AB:
\(1\left(x+2\right)-2\left(y-1\right)=0\Leftrightarrow x-2y+4=0\)
Phương trình đường thẳng d qua C và vuông góc AB:
\(2\left(x+1\right)+1\left(y-2\right)=0\Leftrightarrow2x+y=0\)
Tọa độ M là nghiệm: \(\left\{{}\begin{matrix}x-2y+4=0\\2x+y=0\end{matrix}\right.\) \(\Rightarrow M\left(-\dfrac{4}{5};\dfrac{8}{5}\right)\)
\(\Rightarrow\overrightarrow{MC}=\left(-\dfrac{1}{5};-\dfrac{2}{5}\right)\Rightarrow MC=\dfrac{\sqrt{5}}{5}\)
Đáp án B