Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn B.
Mỗi 60 giây = 1 phút thì kim giây quay được 1 vòng (theo chiều kim đồng hồ quay)
Từ 0 đến 9 giờ là 9 giờ = 540 phút
Do đó kim giây quay được 540 vòng.
Tham khảo:
Giả sử chiếc đu quay quay theo chiều kim đồng hồ.
Gọi M là vị trí của cabin, M’ là vị trí của cabin sau 20 phút và các điểm A A’, B, H như hình dưới.
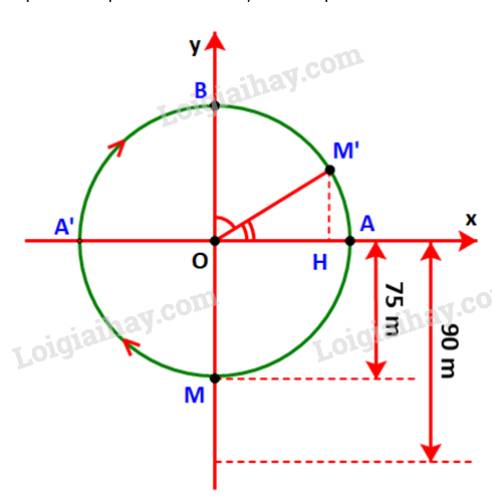
Vì đi cả vòng quay mất 30 phút nên sau 20 phút, cabin sẽ đi quãng đường bằng \(\frac{2}{3}\) chu vi đường tròn.
Sau 15 phút cabin đi chuyển từ điểm M đến điểm B, đi được \(\frac{1}{2}\) chu vi đường tròn.
Trong 5 phút tiếp theo cabin đi chuyển từ điểm B đến điểm M’ tương ứng \(\frac{1}{6}\) chu vi đường tròn hay \(\frac{1}{3}\) cung .
Do đó: \(\widehat {BOM'} = \frac{1}{3}{.180^o} = {60^o}\)\( \Rightarrow \widehat {AOM'} = {90^o} - {60^o} = {30^o}.\)
\( \Rightarrow M'H = \sin {30^o}.OM' = \frac{1}{2}.75 = 37,5\left( m \right).\)
\( \Rightarrow \) Độ cao của người đó là: 37,5 + 90 = 127,5 (m).
Vậy sau 20 phút quay người đó ở độ cao 127,5 m.
Phép đo của các nhà thiên văn có sai số tuyệt đối không vượt quá \(\frac{1}{4}\) ngày, có nghĩa là không vượt quá 360 phút. Phép đo của Hùng có sai số tuyệt đối không vượt quá 1 phút. Nếu chỉ so sánh 360 phút và 1 phút thì có thể dẫn đến hiểu rằng phép đo của bạn Hùng chính xác hơn phép đo của các nhà thiên văn. Tuy nhiên, \(\frac{1}{4}\) ngày hay 360 phút là độ chính xác của phép đo một chuyển động trong 365 ngày, còn 1 phút là độ chính xác của phép đo một chuyển động trong 15 phút. So sánh hai tỉ số \(\frac{{\frac{1}{4}}}{{365}} = \frac{1}{{1460}} = 0,0006849...\) và\(\frac{1}{{15}} = 0,0666...\) , ta thấy rằng phép đo của các nhà thiên văn chính xác hơn nhiều.
Chọn A.
Trong 30 phút mũi kim giờ chạy trên đường tròn có bán kính 10,57 cm và đi được cung có số đo là π/24
Do đó; độ dài đoạn đường mũi kim giờ đi được là 
.
Số giờ ô tô đi từ tỉnh a đến tỉnh b là:
9 giờ 51 phút - 7 giờ 15 phút = 2 giờ 36 phút = 2,6h
Độ dài quãng đường từ tỉnh a đến tỉnh b là:
S= v.t= 45.2,6= 117 (km)
Số giờ ô tô đi từ tỉnh b về tỉnh a là:
S= v.t => t= S: v= 117:52= 2,25h= 2 giờ 15 phút
Ô tô về a lúc:
9 giờ 51 phút + 35 phút + 2 giờ 15 phút = 12 giờ 41 phút
Đáp số: 12 giờ 41 phút
thời gian đi: t1=9,85-7,25=2,6(h)
độ dài quảng đường ab: Sab=45*2.6=117(km)
thời gian nghỉ: t2=35'=7/12(h)
thời gian về: t3=117:52=2,25(h)
tổng thời gian đi ab và ba: t=t1+t2+t3=2,6+7/12+2,25=163/30(h)
thời gian ô tô về đến a: 7,25+163/30 =12,68(h)
Sau khi được ném đi, quỹ đạo chuyển động của chiếc đĩa nằm trên tiếp tuyến của đường tròn tâm I tại điểm M.
Vậy quỹ đạo chuyển động của chiếc đĩa nằm trên đường thẳng có phương trình là:
\(\begin{array}{l}\left( {\frac{{\sqrt {39} }}{{10}} - 0} \right)\left( {x - \frac{{\sqrt {39} }}{{10}}} \right) + \left( {2 - \frac{3}{2}} \right)\left( {y - 2} \right) = 0\\ \Leftrightarrow \frac{{\sqrt {39} }}{{10}}\left( {x - \frac{{\sqrt {39} }}{{10}}} \right) + \frac{1}{2}\left( {y - 2} \right) = 0\\ \Leftrightarrow \sqrt {39} x + 5y - 13,9 = 0\end{array}\)
Sau khi được ném đi, quỹ đạo chuyển động của chiếc đĩa nằm trên tiếp tuyến của đường tròn tâm I tại điểm M.
Vậy quỹ đạo chuyển động của chiếc đĩa nằm trên đường thẳng có phương trình là:
\(\left(\dfrac{\sqrt{39}}{10}-0\right)\left(x-\dfrac{\sqrt{39}}{10}\right)+\left(2-\dfrac{3}{2}\right)\left(y-2\right)=0\\ \Leftrightarrow\dfrac{\sqrt{39}}{10}\left(x-\dfrac{\sqrt{39}}{10}\right)+\dfrac{1}{2}\left(y-2\right)=0\\ \Leftrightarrow\sqrt{39}x+5y-13,9=0\)
Người đó chuyển động theo quỹ đạo đường tròn nên để xác định phương trình quỹ đạo chuyển động của người đó ta cần phải lập phương trình đường tròn.
XÉT CÁC KHOẢNG PHÚT TRONG ĐỒNG HỒ, TA NHÂN THẤY ĐỒNG HỒ CÓ 60 KHOẢNG
TRONG 1 GIỜ THÌ KIM PHÚT QUAY ĐƯỢC 60 KHOẢNG TƯƠNG ĐƯƠNG VỚI 1 VÒNG VÀ KIM GIỜ QUAY ĐƯỢC 5 KHOẢNG
=> KIM GIỜ QUAY ĐƯỢC 5/60 HAY 1/12 VÒNG
Cảm ơn bạn nhé!