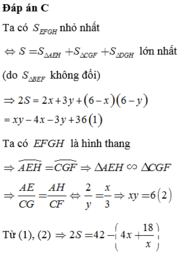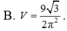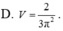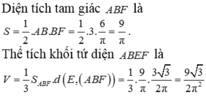Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

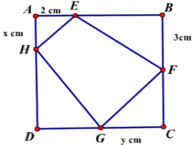
Ta có SEFGH nhỏ nhất ↔ S = S A E H + S C G F + S D G H lớn nhất
Tính được 2S= 2x+ 3y+ (6-x) (6-y) = xy-4x-3y+36 (1)
Mặt khác ∆ AEH đồng dạng ∆CGF nên A E C G = A H C F ⇒ x y = 6
Từ (1) và (2) suy ra 2S = 42 - ( 4 x - 18 x )
Ta có 2S nhỏ nhất khi và chỉ khi 4 x - 18 x nhỏ nhất.
Biểu thức nhỏ nhất 4 x - 18 x nhỏ nhất ↔ 4 x = 18 x ⇒ x = 3 2 2 ⇒ y = 2 2
Vậy x+y = 3 2 2 + 2 2
Chọn D.

đường thẳng AB qua H và vuông HE nên ptdt AB : x+2=0
đường thẳng AD qua K và vuông KE nên ptdt AD : -y+4=0
Tọa độ A là nghiệm của hệ : \(\begin{cases}x+2=0\\-y+4=0\end{cases}\) \(\Leftrightarrow\begin{cases}x=-2\\y=4\end{cases}\) vậy A(-2;4)
\(\overrightarrow{HE}=\left(4;0\right)\Rightarrow HE=AK=4;\overrightarrow{KE}=\left(0;-1\right)\Rightarrow KE=1\) . Vậy \(\overrightarrow{AK}=\frac{4}{5}\overrightarrow{AD}\) , có \(\overrightarrow{AK}=\left(4;0\right);\overrightarrow{AD}=\left(x_D+2;y_D-4\right)\) ta có hê : \(\begin{cases}4=\frac{4}{5}\left(x_D+2\right)\\0=\frac{4}{5}\left(y_D-4\right)\end{cases}\) \(\Leftrightarrow\begin{cases}x=3\\y=4\end{cases}\)Vậy D(3;4)
ptdt DE đi qua D và E nên ta có ptdt: x-y+1=0
Tọa độ điểm B là nghiêm của hệ phương trình đường thẳng DE và AB: \(\begin{cases}x-y=-1\\x=-2\end{cases}\) \(\Leftrightarrow\begin{cases}x=-2\\y=-1\end{cases}\) Vậy B(-2;-1)
Goi O(xo ;yo) là giao điểm của BD và AC. ta có : \(\begin{cases}x_o=\frac{-2+3}{2}=\frac{1}{2}\\y_o=\frac{-1+4}{2}=\frac{3}{2}\end{cases}\) Vậy O(\(\frac{1}{2};\frac{3}{2}\)) . O là trung điểm của AC nên C(3;-1)

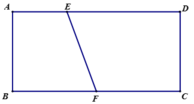
vì (SBI) và (SCI) cùng vuông góc với( ABCD) nên SI vuông với (ABCD) ,ke Az song song với SI và chọn gốc tọa độ tại A