Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

S A B C D M O N H 45 ❤sin45=\(\dfrac{SO}{SM}\) => SO=sin45 . SM= \(\dfrac{\sqrt{2}}{2}.\dfrac{a\sqrt{3}}{2}\) = \(\dfrac{a\sqrt{6}}{4}\)
OM= \(\sqrt{SM^2-SO^2}\) = \(\dfrac{a\sqrt{6}}{4}\)
BC = 2OM => BC=\(\dfrac{a\sqrt{6}}{2}\)
V = \(\dfrac{1}{3}.AB.BC.SO=\dfrac{1}{3}.a.\dfrac{a\sqrt{6}}{2}.\dfrac{a\sqrt{6}}{4}=\dfrac{a^3}{4}\)
❤ta có: SM⊂ (SAB) (1)
mà: \(\left\{{}\begin{matrix}NC//AB\\AB\subset\left(SAB\right)\end{matrix}\right.\) => NC// (SAB) (2)
từ (1) và (2) => SM//NC
\(d_{\left(SM,NC\right)}=d_{\left(NC,\left(SAB\right)\right)}=d_{\left(N,\left(SAB\right)\right)}=2d_{\left(O,\left(SAB\right)\right)}\)
+kẻ OH⊥SM
+ Ta có: \(\left\{{}\begin{matrix}AB\perp OM\\AB\perp SO\end{matrix}\right.\) => AB ⊥ (SOM) \(\supset OH\)
=> \(\left\{{}\begin{matrix}OH\perp AB\\OH\perp SM\end{matrix}\right.\) => OH⊥(SAB)
➜d(O,(SAB)) =OH
OH=\(\dfrac{OM.SO}{\sqrt{OM^2+SO^2}}\)\(\dfrac{a\sqrt{3}}{4}\)
➜d(N,(SAB)) =d(SM,NC)= \(\dfrac{a\sqrt{3}}{2}\)

Đáp án D
Từ O kẻ OH vuông góc với SC, ta có S C ⊥ ( B D H )
Ta có V S . A H D V S . A C D = S H S C , V S . A H B V S . A C B = S H S C
mà V S . A C D = V S . A C B = 1 2 V S . A B C D = V 2
nên V S . A H D + V S . A H B V 2 = 2 S H S C
⇔ V S . A B H D V = S H S C
Có
B
C
⊥
(
S
A
M
)
nên
![]()
⇒ S A = 3 a 2
Mặt khác: ∆ C A S ~ ∆ C H O
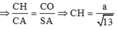
Suy ra S H S C = S C - H C S C = 1 - H C S C = 11 13
⇒ V S . A B H D = 11 13 V
Do đó
V H . B C D = V - V S . A B H D = V = 11 12 V = 2 13 V

Đáp án C
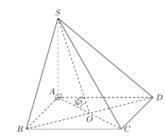
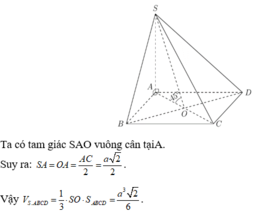
Ta có tam giác SAO vuông cân tạiA.
Suy ra:
S
A
=
O
A
=
A
C
2
=
a
2
2
Vậy : V S . A B C D = 1 3 . S O . S A B C D = a 3 2 6

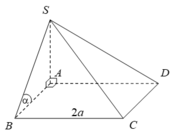
Ta có: SA ⊥ (ABCD) SA ⊥ AB
Mặt phẳng (SAB) tạo với đáy một góc 60° nên
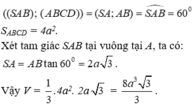

Gợi ý xem bạn làm được ko, ko thì để mình trình bày luôn
Kẻ \(KC\perp HD;KC\cap HD=\left\{K\right\}\)
\(\left\{{}\begin{matrix}KC\perp HD\\KC\perp SH\end{matrix}\right.\Rightarrow KC\perp\left(SHD\right)\Rightarrow\left(SKC\right)\perp\left(SHD\right)\)
Kẻ \(CI\perp SK;CI\cap SK=\left\{I\right\}\Rightarrow CI\perp\left(SHD\right)\Rightarrow CI\perp\left(SHD\right)\)
\(\Rightarrow\left(SC,\left(SHD\right)\right)=\left(SC,SI\right)\)


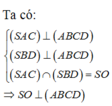
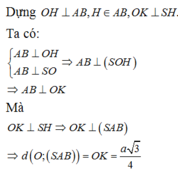

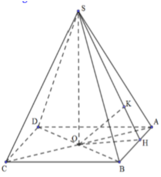

Gọi H là điểm gia của AC và MD.
Ta có : (SAC) giao (SMD) = SH, cùng vuông góc vuối (ABCD)
=> SH là đường cao.
Kẻ HK vuông góc với AB, có AB vuông góc với (SKH) => góc tạo bởi (ABCD) và (SAB)
=> SKH = 600
Có tam giác ABD đều tại A => AO = \(\frac{a\sqrt{3}}{8}\)
=> tan (SKH) = SH/SK => SH = \(\frac{3a}{8}\Rightarrow V=\frac{\sqrt{3}a^3}{16}\)
=> cos OM và OA là \(\frac{a\sqrt{13}}{4}\)
bạn ơi. đề bài là cosin của OM và SA