
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: A=căn x-1
=>\(\left(\sqrt{x}-1\right)\cdot\dfrac{\sqrt{x}}{3}-\left(\sqrt{x}-1\right)=0\)
=>(căn x-1)(1/3*căn x-1)=0
=>x=1 hoặc x=9
b: \(B=\dfrac{x+2\sqrt{x}+4-x+\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\)
\(=\dfrac{3\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}=\dfrac{3}{x-\sqrt{x}+1}\)
c: \(A\cdot B< =\dfrac{\sqrt{x}-1}{x-\sqrt{x}+1}\)
=>\(\dfrac{3\left(x-\sqrt{x}\right)}{3\left(x-\sqrt{x}+1\right)}< =\dfrac{\sqrt{x}-1}{x-\sqrt{x}+1}\)
=>x-2căn x+1<=0
=>(căn x-1)^2<=0
=>x=1

`(3x+2)/3 <= (x-4)/7`
`<=>7(3x+2) <= 3(x-4)`
`<=>21x+14 <= 3x-12`
`<=> 18x <=-26`
`<=>x <= -13/9`
Vậy `x<=-13/9`.

Bài 3:
a: Ta có: \(4x\left(x+1\right)=8\left(x+1\right)\)
\(\Leftrightarrow\left(x+1\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=2\end{matrix}\right.\)
b: Ta có: \(x\left(x-1\right)+2\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
c: Ta có: \(2x\left(x-2\right)-\left(x-2\right)^2=0\)
\(\Leftrightarrow\left(x-2\right)\left(2x-x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)

a:=>(x-3)(2x-5)=0
=>x=3 hoặc x=5/2
b: =>(x-2)(x+2)+(x-2)(2x-3)=0
=>(x-2)(x+2+2x-3)=0
=>(x-2)(3x-1)=0
=>x=1/3 hoặc x=1
c: =>(2x+5-x-2)(2x+5+x+2)=0
=>(x+3)(3x+7)=0
=>x=-7/3 hoặc x=-3
d: =>(x-2)(x-3)=0
=>x=2 hoặc x=3
e: =>(x+3)(x^2-3x+9+x-9)=0
=>(x+3)(x^2-2x)=0
=>\(x\in\left\{0;2;-2\right\}\)
f: =>(10x-5)^2=(2x-4)^2
=>(10x-5-2x+4)(10x-5+2x-4)=0
=>(8x-1)(12x-9)=0
=>x=3/4 hoặc x=1/8

Vì \(RN=NQ,QM=QP\Rightarrow MN\) là đường trung bình tam giác PQR
\(\Rightarrow PQ=2MN=2.22,125=44,25\)


\(\left(2x-5\right).2=\left(x+2\right).3\)
\(\Rightarrow4x-10=3x+6\)
\(\Rightarrow x=16\)
\(\dfrac{2x+5}{3}=\dfrac{x+2}{2}\)
MTC : 6
Quy đồng mẫu thức :
\(\Rightarrow\) \(\dfrac{2\left(2x+5\right)}{6}=\)\(\dfrac{3\left(x+2\right)}{6}\)
Suy ra : 2(2x + 5) = 3(x + 2)
\(\Leftrightarrow\) 4x + 10 = 3x + 6
\(\Leftrightarrow\) 4x + 10 - 3x - 6 = 0
\(\Leftrightarrow\) x + 4 = 0
\(\Leftrightarrow\) x = - 4
Vậy S = \(\left\{-4\right\}\)
Chúc bạn học tốt

Dài như này là mình xoá đấy ak !! Bạn f biết rằng vào năm học r, mọi người đều có bt riêng :((( nếu muốn nhận sự trợ giúp nhanh nhất thì f đăng lẻ ra chứ ak?

`(3x+2)/3 <= (x-4)/7`
`<=>7(3x+2) <= 3(x-4)`
`<=> 21x+14<=3x-12`
`<=>18x <= -26`
`<=> x <=-13/9`
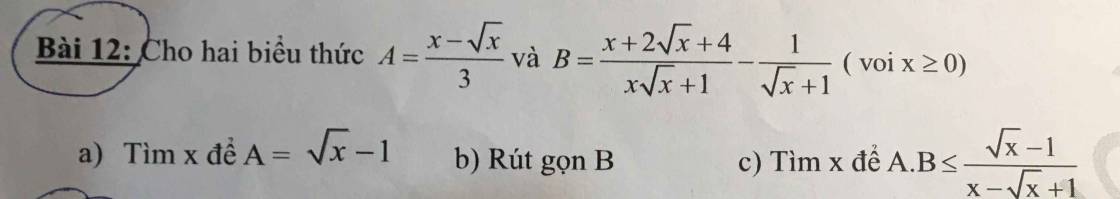


 help em vs mn ơi
help em vs mn ơi

a)
=25
b)
=1
HT
a, \(\left(x-y\right)^2=\left(x+y\right)^2-4xy\)
\(\Rightarrow49-48=1\)
b, \(3\left(x^2+y^2\right)-2\left(x^3+y^3\right)=3\left[\left(x+y\right)^2-2xy\right]-2\left[\left(x+y\right)\left(x^2-xy+y^2\right)\right]\)
\(=3\left[\left(x+y\right)^2-2xy\right]-2\left(x+y\right)\left[\left(x+y\right)^2-3xy\right]\)
Thiếu xy nhé