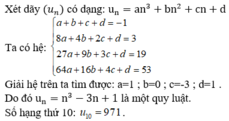A
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
13 tháng 1 2019
Ta có
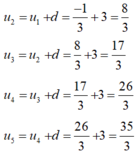
Quy luật: kể từ số thứ 2, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với 4. Năm số hạng tiếp của dãy theo quy luật đó: 15; 19; 23; 27; 31
HQ
Hà Quang Minh
Giáo viên
25 tháng 8 2023
a, Quy luật: Mỗi số hạng kể từ số thứ hai bằng số hạng đứng trước nó chia cho 2.
Vậy ba số hạng tiếp theo là: \(a_5=1;a_6=\dfrac{1}{2};a_7=\dfrac{1}{4}\)
b, Các số hạng của dãy số có dạng \(2^n\) với số mũ của số liền sau ít hơn số mũ của số liền trước 1 đơn vị.
Vậy ta có thể viết ba số hạng tiếp theo là: \(a_5=a^0;a_6=a^{-1};a_7=a^{-2}\)
TH
Cho dãy số 4 số đầu là -1;3;19;53.hãy tìm ra quy luật của dãy số trên và viết số hạng thứ 10 của dãy
0
AH
Akai Haruma
Giáo viên
31 tháng 1 2018
Lời giải:
a) Từ công thức truy hồi \(u_{n+1}=u_n+n^3\) suy ra:
\(u_1=1\) (theo giả thiết)
\(u_2=u_1+1^3=2\)
\(u_3=u_2+2^3=2+2^3=10\)
\(u_4=u_3+3^3=37\)
\(u_5=u_4+4^3=101\)
b) Ta sẽ chỉ ra công thức tổng quát của dãy là:
\(u_n=1+1^3+2^3+...+(n-1)^3\)
Thật vậy:
Với \(n=2\Rightarrow u_2=1+1^3=2\) (đúng)
Với \(n=3\Rightarrow u_3=1+1^3+2^3=10\) (đúng)
....
Giả sử công thức đúng với \(n=k\), tức là:
\(u_k=1+1^3+2^3+...+(k-1)^3\)
Ta chứng minh nó cũng đúng với \(n=k+1\)
Thật vậy:
\(u_{k+1}=u_k+k^3=1+1^3+2^3+...+(k-1)^3+k^3\)
Do đó công thức đúng với $n=k+1$
Do đó ta có \(u_n=1+1^3+2^3+...+(n-1)^3=1+\left(\frac{n(n-1)}{2}\right)^2\)
4 tháng 9 2017
ADCT: sin2a=2sina.cosa
cos2a=2cos2a-1 (a ở đây có thể là: x, 2x,3x, pi/2-x,......)
a)
pt<=>4sin2x.cos2x=cos2.(\(\dfrac{\Pi}{4}\)-4x)
<=>2sin4x=2cos2(\(\dfrac{\Pi}{4}\)-4x)-1
<=>2sin4x=2.(\(\dfrac{\sqrt{2}}{2}\))2.(cos4x+sin4x)2-1
<=>2sin4x=(cos24x+sin24x)+2sin4x.cos4x-1
<=>2sin4x=1+2sin4x.cos4x-1
<=>2sin4x(1-cos4x)=0
Tới đây đơn giản rồi bạn tự giải đi!
4 tháng 9 2017
b)
Pt<=>(sinx.cos\(\dfrac{\Pi}{2}\)+cosx.sin\(\dfrac{\Pi}{2}\))4-sin4x=sin4x
<=>cos4x-sin4x=sin4x
<=>(cos2x-sin2x)(cos2x+sin2x)-sin4x=0
cos2x+sin2x=1, cos2x-sin2x=cos2x
<=>cos2x-2sin2x.cos2x=0
<=>cos2x(1-2sin2x)=0
Tự giải dc rồi chứ????
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
a, Ta có: \(\dfrac{4}{2}=2;\dfrac{8}{4}=2;\dfrac{16}{8}=2;\dfrac{32}{16}=2;\dfrac{64}{32}=2\)
b, Ta thấy:
i, Số sai bằng số liền trước nhân với 2.
ii, Số sau bằng số liền trước nhân với \(\dfrac{1}{2}\)
iii, Số sau bằng số liền trước nhân với -3.
Điểm giống nhau của các dãy số này là số sau bằng số liền trước nhân với một số không đổi.
