K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
11 tháng 1 2019
Lời giải:
\(|x-2019|-|x-1|=0\)
\(\Leftrightarrow |x-2019|=|x-1|\)
\(\Rightarrow \left[\begin{matrix} x-2019=x-1\\ x-2019=-(x-1)=1-x\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} 2019=1(\text{vô lý})\\ x=1010\end{matrix}\right.\)
Vậy $x=1010$
.
30 tháng 3 2017
Bài 4:
\(M+\left(5x^2-2y^3\right)=10x^2+4y^3\)
\(=>M=\left(10x^2+4y^3\right)-\left(5x^2-2y^3\right)\)
\(M=10x^2+4y^3-5x^2+2y^3\)
\(M=\left(10x^2-5x^2\right)+\left(4y^3+2y^3\right)\)
\(M=5x^2+6y^3\)
Vì \(M+N=8x^2-3y^2\)
\(=>N=\left(8x^2-3y^2\right)-\left(5x^2+6y^3\right)\)
\(N=8x^2-3y^2-5x^2-6y^3\)
\(N=\left(8x^2-5x^2\right)-3y^2-6y^3\)
\(=>N=3x^2-3y^2-6y^3\)
30 tháng 3 2017
lần sau cái đề bài nó ngắn thì viết ra, đọc thế này mỏi cổ lắm, bộ ko type ra đc à @Lucy Châu
2 tháng 5 2020
Ta có: \(\frac{x}{1,75}\)=\(\frac{y}{0,75}\) và x-y = 4
⇒ \(\frac{x}{1,75}\)=\(\frac{y}{0,75}\)=\(\frac{x-y}{1,75-0,75}\)=\(\frac{4}{1}\)=4
⇒\(\frac{x}{1,75}\)=4 ⇔ x = 4 . 1,75 = 7
⇒\(\frac{y}{0,75}\)= 4 ⇔ y = 4 . 0,75 = 3
Vậy x = 7 ; y = 3
NG
3
S
8 tháng 12 2018
\(\left(x-\dfrac{1}{5}\right)^2=\dfrac{4}{25}\Leftrightarrow\left(x-\dfrac{1}{5}\right)^2=\left(\dfrac{2}{5}\right)^2\)
\(\Leftrightarrow x-\dfrac{1}{5}=\dfrac{2}{5}\Leftrightarrow x=\dfrac{3}{5}\)
8 tháng 12 2018
pt \(\Leftrightarrow\)\(\left[{}\begin{matrix}x-\dfrac{1}{5}=\dfrac{2}{5}\\x-\dfrac{1}{5}=-\dfrac{2}{5}\end{matrix}\right.\)\(\Leftrightarrow\)\(\left[{}\begin{matrix}x=\dfrac{3}{5}\\x=-\dfrac{1}{5}\end{matrix}\right.\)
20 tháng 8 2016
\(\left(x-\frac{1}{4}\right)^2=\frac{1}{9}\)
\(\left(x-\frac{1}{4}\right)^2=\left(\frac{1}{3}\right)^2\)
\(\Rightarrow\left|x-\frac{1}{4}\right|=\frac{1}{3}\)
\(x-\frac{1}{4}=\frac{1}{3}\)HOẶC \(x-\frac{1}{4}=-\frac{1}{3}\)
\(x=\frac{7}{12}\)HOẶC \(x=-\frac{1}{12}\)
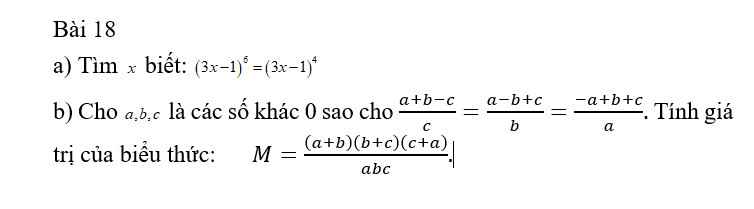
a) \(\left(3x-1\right)^6=\left(3x-1\right)^4\)
\(\Rightarrow\left[{}\begin{matrix}3x-1=0\\3x-1=1\\3x-1=-1\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=\dfrac{2}{3}\\x=0\end{matrix}\right.\)
b) Áp dụng t/c dtsbn:
\(\dfrac{a+b-c}{c}=\dfrac{a-b+c}{b}=\dfrac{-a+b+c}{a}=\dfrac{a+b+c}{a+b+c}=1\)
\(\Rightarrow\left\{{}\begin{matrix}a+b-c=c\\a-b+c=b\\-a+b+c=a\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}a+b=2c\\a+c=2b\\b+c=2a\end{matrix}\right.\)
\(\Rightarrow M=\dfrac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{abc}=\dfrac{2a.2b.2c}{abc}=8\)
Giúp Mình Với
Mình Đang Cần Gấp