
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


8.
Hàm có 1 điểm cực đại \(\left(x=-1\right)\)
9.
Hàm có 1 điểm cực tiểu (\(x=-1\))
14.
\(y'=\dfrac{2x\left(x+1\right)-\left(x^2+3\right)}{\left(x+1\right)^2}=\dfrac{x^2+2x-3}{\left(x+1\right)^2}\)
\(y'=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)
Xét dấu y' trên trục số:
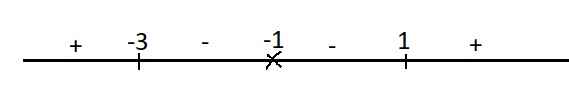
Từ dấu của y' ta thấy \(x=1\) là điểm cực tiểu
\(\Rightarrow y_{CT}=y\left(1\right)=2\)

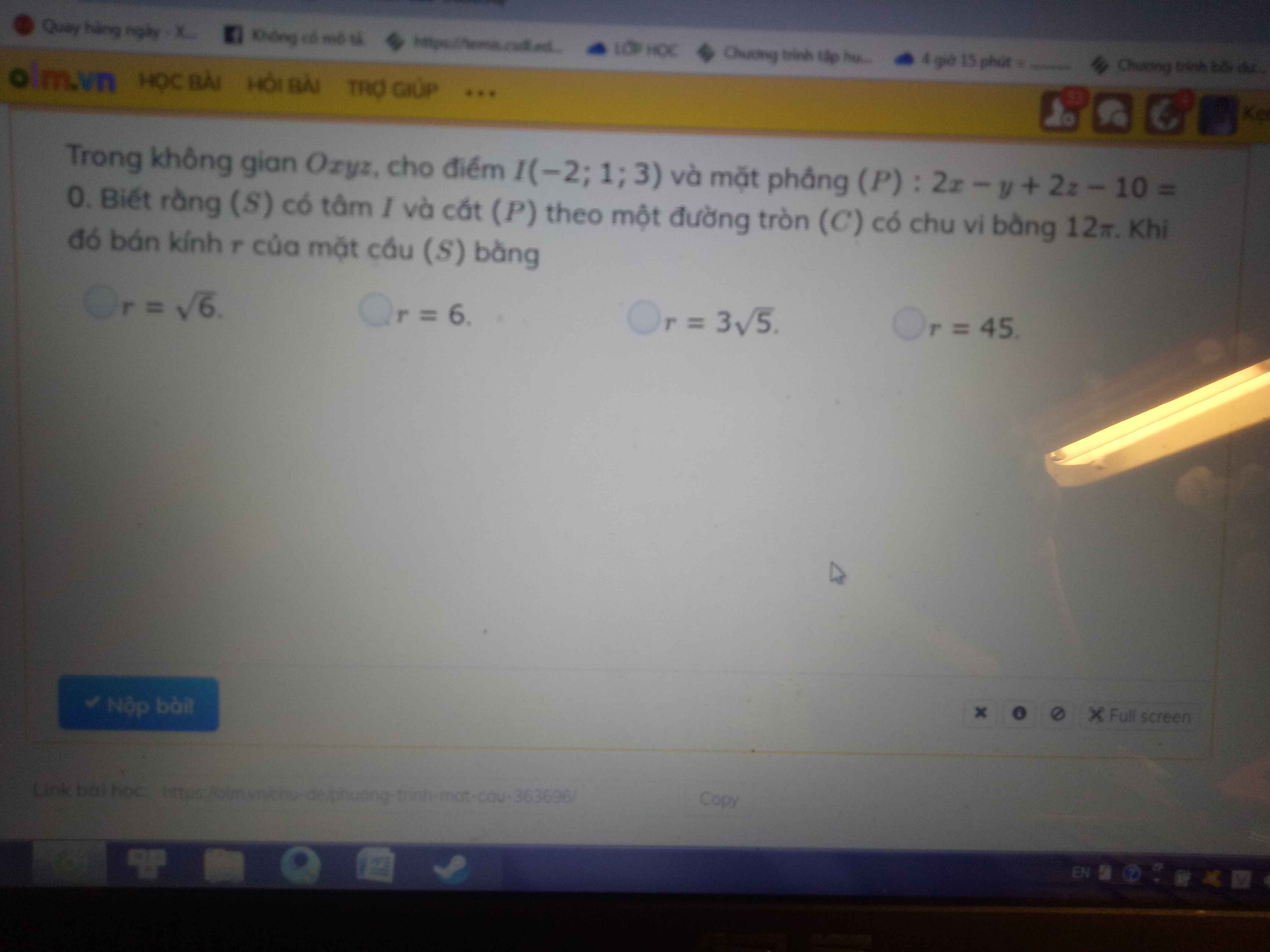
Gọi R là bán kính (C) \(\Rightarrow2\pi R=12\pi\Rightarrow R=6\)
Gọi \(J\) là tâm (C) \(\Rightarrow IJ\perp\left(P\right)\Rightarrow IJ=d\left(I;\left(P\right)\right)\)
\(d\left(I;\left(P\right)\right)=\dfrac{\left|2.\left(-2\right)-1.1+2.3-10\right|}{\sqrt{2^2+\left(-1\right)^2+2^2}}=3\)
\(\Rightarrow IJ=3\)
Áp dụng định lý Pitago:
\(r^2=IJ^2+R^2=45\Rightarrow r=3\sqrt{5}\)
Đường tròn (C)(C) có bán kính R = 6R=6.
d(I,(P))=3.
Mặt cầu (S) cắt mặt phẳng (P) theo một đường tròn
(C)(C) nên có bán kính:
r=\(\sqrt{R^2+(d(I,(P)))^2 } =3\sqrt{5}
\)(P(P) theo một đường tròn (C)(C) nên có bán kính:(S)(S) cắt mặt phẳng (P)

1.
\(y'=6x^2+6\left(m-1\right)x+6\left(m-2\right)=6\left(x+1\right)\left(x+m-2\right)\)
\(y'=0\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-m+2\end{matrix}\right.\)
Phương trình nghịch biến trên đoạn có độ dài lớn hơn 3 khi:
\(\left|-1-\left(-m+2\right)\right|>3\)
\(\Leftrightarrow\left|m-3\right|>3\Rightarrow\left[{}\begin{matrix}m>6\\m< 0\end{matrix}\right.\)
2.
\(y'=-3x^2+6x+m-1\)
\(\Delta'=9+3\left(m-1\right)>0\Rightarrow m>-2\)
Gọi \(x_1;x_2\) là 1 nghiệm của pt \(-3x^2+6x+m-1=0\Rightarrow\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=\dfrac{-m+1}{3}\end{matrix}\right.\)
Hàm đồng biến trên đoạn có độ dài lớn hơn 1 khi:
\(\left|x_1-x_2\right|>1\)
\(\Leftrightarrow\left(x_1-x_2\right)^2>1\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2>1\)
\(\Leftrightarrow4-\dfrac{-4m+4}{3}>1\)
\(\Rightarrow m>-\dfrac{5}{4}\) \(\Rightarrow m=-1\)
Có đúng 1 giá trị nguyên âm của m thỏa mãn
3.
\(y'=x^2+6\left(m-1\right)x+9\)
\(\Delta'=9\left(m-1\right)^2-9>0\Rightarrow\left[{}\begin{matrix}m>1\\m< 0\end{matrix}\right.\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-6\left(m-1\right)\\x_1x_2=9\end{matrix}\right.\)
\(\left|x_1-x_2\right|=6\sqrt{3}\)
\(\Leftrightarrow\left(x_1-x_2\right)^2=108\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=108\)
\(\Leftrightarrow36\left(m-1\right)^2-36=108\)
\(\Rightarrow\left(m-1\right)^2=4\Rightarrow\left[{}\begin{matrix}m=3\\m=-1\end{matrix}\right.\)
Có 1 giá trị nguyên âm của m thỏa mãn



Giả sử z = x + yi (x, y ∈ R), khi đó số phức z được biểu diễn bởi điểm M(x, y) trên mặt phẳng tọa độ Oxy.
a) Trên hình 71.a (SGK), điểm biểu diễn ở phần gạch chéo có hoành độ có hoành độ x ≥ 1, tung độ y tùy ý.
Vậy số phức có phần thực lớn hơn hoặc bằng -1 có điểm biểu diễn ở hình 71.a (SGK)
b) Trên hình 71.b(SGK), điểm biểu diễn có tung độ y ∈ [1, 2], hoành độ x tùy ý.
Vậy số phức có phần ảo thuộc đoạn [-1, 2]
c) Trên hình 71.c (SGK), hình biểu diễn z có hoành độ x ∈ [-1, 1] và x2 + y2 ≤ 4 (vì |z| ≤ 4.
Vậy số phực có phần thực thuộc đoạn [-1, 1] và môdun không vượt quá 2.

31.
\(y'=\dfrac{1+m}{\left(x+1\right)^2}\)
Hàm đồng biến trên các khoảng xác định khi:
\(\dfrac{1+m}{\left(x+1\right)^2}>0\Rightarrow m>-1\) (C)
32.
\(y'=\dfrac{4-m^2}{\left(x+4\right)^2}\)
Hàm đồng biến trên các khoảng xác định khi:
\(4-m^2>0\Rightarrow-2< m< 2\)
\(\Rightarrow m=\left\{-1;0;1\right\}\)
Có 3 giá trị nguyên của m
33.
\(y'=\dfrac{m-1}{\left(x+1\right)^2}\)
Hàm đồng biến trên từng khoảng xác định khi:
\(m-1>0\Rightarrow m>1\)
34.
\(y'=\dfrac{2m-1}{\left(x+2m\right)^2}\)
Hàm đồng biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}2m-1>0\\-2m>-3\end{matrix}\right.\) \(\Rightarrow\dfrac{1}{2}< m< \dfrac{3}{2}\)
\(\Rightarrow m=1\)
Có 1 giá trị nguyên của m

\(\left(1-\dfrac{1}{2}\right)\):\(\left(1-\dfrac{1}{3}\right)\):\(\left(1-\dfrac{1}{4}\right)\):\(\left(1-\dfrac{1}{5}\right)\):\(\left(1-\dfrac{1}{6}\right)\):\(\left(1-\dfrac{1}{7}\right)\)
=\(\left(\dfrac{2-1}{2}\right)\):\(\left(\dfrac{3-1}{3}\right)\):\(\left(\dfrac{4-1}{4}\right)\):\(\left(\dfrac{5-1}{5}\right)\):\(\left(\dfrac{6-1}{6}\right)\)
=\(\dfrac{1}{2}\):\(\dfrac{2}{3}\):\(\dfrac{3}{4}\):\(\dfrac{4}{5}\):\(\dfrac{5}{6}\)
=\(\dfrac{1.\left(3.4.5\right)6}{\left(3.4.5\right)\left(2.2\right)}\)
=\(\dfrac{6}{2.2}=\dfrac{3}{2}\)










phương trình hoành độ giao điểm :
\(-2x+2=x^2+x+2\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\Rightarrow y=2\\x=-3\Rightarrow y=8\end{matrix}\right.\)