Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có:
\(\left\{{}\begin{matrix}M\in\left(MCD\right)\\M\in AB\subset\left(NAB\right)\end{matrix}\right.\)\(\Rightarrow M\in\left(MCD\right)\cap\left(NAB\right)\)
\(\left\{{}\begin{matrix}N\in CD\subset\left(MCD\right)\\N\in\left(NAB\right)\end{matrix}\right.\)\(\Rightarrow N\in\left(MCD\right)\cap\left(NAB\right)\)
\(\Rightarrow MN=\left(MCD\right)\cap\left(NAB\right)\)
b) Trong mp(BCD), gọi \(P=NG\cap BD\)
Trong mp(BAD), gọi \(Q=PM\cap AD\)
Ta có:
\(\left\{{}\begin{matrix}N\in\left(GMN\right)\\N\in CD\subset\left(ACD\right)\end{matrix}\right.\)\(\Rightarrow N\in\left(GMN\right)\cap\left(ACD\right)\)
Ta có:
\(\left\{{}\begin{matrix}Q\in MP\subset\left(GMN\right)\\Q\in AD\subset\left(ACD\right)\end{matrix}\right.\)\(\Rightarrow Q\in\left(GMN\right)\cap\left(ACD\right)\)
\(\Rightarrow NQ=\left(GMN\right)\cap\left(ACD\right)\)

a) Gọi \(N=DK\cap AC;M=DJ\cap BC\).
Ta có \(\left(DJK\right)\cap\left(ABC\right)=MN\Rightarrow MN\subset\left(ABC\right)\)
Vì \(L=\left(ABC\right)\cap JK\) nên dễ thấy \(L=JK\cap MN\)


a) Gọi N = DK ∩ AC; M = DJ ∩ BC.
Ta có (DJK) ∩ (ABC) = MN ⇒ MN ⊂ (ABC).
Vì L = (ABC) ∩ JK nên dễ thấy L = JK ∩ MN.
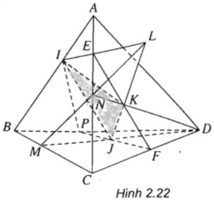
b) Ta có I là một điểm chung của (ABC) và (IJK).
Mặt khác vì L = MN ∩ JK mà MN ⊂ (ABC) và JK ⊂ (IJK) nên L là điểm chung thứ hai của (ABC) và (IJK), suy ra (IJK) ∩ (ABC) = IL.
Gọi E = IL ∩ AC; F = EK ∩ CD. Lí luận tương tự ta có EF = (IJK) ∩ (ACD).
Nối FJ cắt BD tại P; P là một giao điểm (IJK) và (BCD).
Ta có PF = (IJK) ∩ (BCD) Và IP = (ABD) ∩ (IJK)

a/ MN chính là giao tuyến đó luôn (N thuộc CD nên N thuộc (MCD), và hiển nhiên N thuộc (NAB), do đó N là 1 điểm chung của (MCD) và (NAB). Tương tự với điểm M)
b/ Trong mặt phẳng (BCD), nối GN kéo dài cắt BC tại E
Trong mặt phẳng (ABC), nối EM kéo dài cắt AC tại F
\(\Rightarrow NF\) là giao tuyến (GMN) và (ACD)

a) Nhận xét:
Do giả thiết cho IJ không song song với CD và chúng cùng nằm trong mặt phẳng (BCD) nên khi kéo dài chúng gặp nhau tại một điểm.
Gọi K = IJ ∩ CD.
Ta có: M là điểm chung thứ nhất của (ACD) và (IJM);
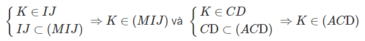
Vậy (MIJ) ∩ (ACD) = MK
b) Với L = JN ∩ AB ta có:
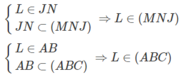
Như vậy L là điểm chung thứ nhất của hai mặt phẳng (MNJ) và (ABC)
Gọi P = JL ∩ AD, Q = PM ∩ AC
Ta có:
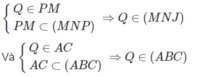
Nên Q là điểm chung thứ hai của (MNJ) và (ABC)
Vậy LQ = (ABC) ∩ (MNJ).
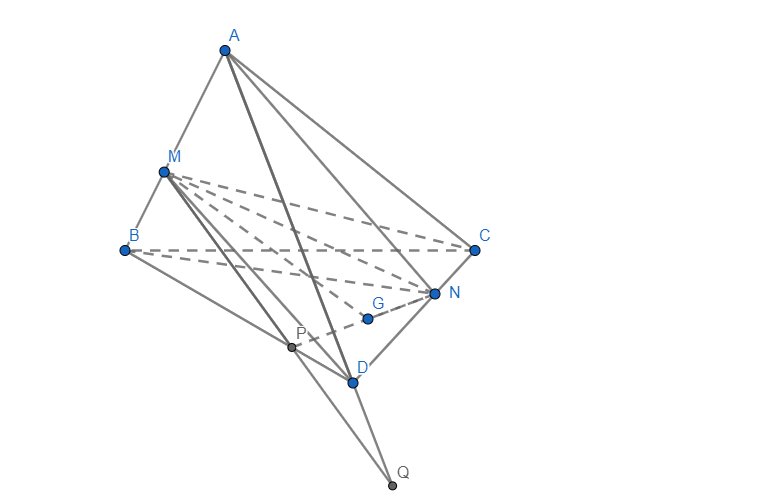



A B C D O N M P Q
Hình hơi rối, chịu khó tưởng tượng
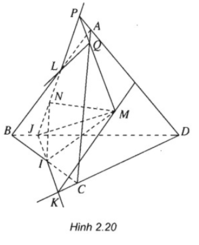
a/ Nối DO cắt BC tại N, nối AN
Trong mặt phẳng \(\left(ADN\right)\) kéo dài \(DM\) cắt \(AN\) tại P
Trong mặt phẳng \(\left(ABC\right)\) nối CP kéo dài cắt AB tại Q
\(\Rightarrow CQ\) là giao tuyến (MCD) và (ABC)
b/ Tương tự câu a
Nối CO cắt BD tại E
Kéo dài CM cắt AE tại F
Nối DF cắt AB tại G
DG là giao tuyến cần tìm