Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khách hàng nam ở khoảng tuổi \(\left[ {40;50} \right)\) mua bảo hiểm nhân thọ nhiều nhất.
Khách hàng nữ ở khoảng tuổi \(\left[ {30;40} \right)\) mua bảo hiểm nhân thọ nhiều nhất.
Ta có thể biết mốt của mẫu số liệu đó.

| Khoảng tuổi | [20;30) | [30;40) | [40;50) | [50;60) | [60;70) |
| Số khách | 3 | 9 | 6 | 4 | 2 |

tham khảo
A là biến cố "Cường đứng đầu hàng", \(P\left(A\right)=\dfrac{6!.C^1_2}{7!}=\dfrac{2}{7}\)
B là biến cố "Trọng đứng đầu hàng", \(P\left(B\right)=\dfrac{6!.C^1_2}{7!}=\dfrac{2}{7}\)
AB là biến cố "Trọng và Cường cùng đứng đầu hàng" \(P\left(AB\right)=\dfrac{2!.5!}{7!}=\dfrac{1}{21}\)
\(A\cup B\)
là biến cố "Có ít nhất một trong hai bạn Cường và Trọng đứng ở đầu hàng"
\(P\left(A\cup B\right)=P\left(A\right)+P\left(B\right)-P\left(A\right).P\left(B\right)=\dfrac{11}{21}\)
THAM KHẢO:
A là biến cố "Cường đứng đầu hàng", P(A)=\(\dfrac{6!.C\dfrac{1}{2}}{7!}=\dfrac{2}{7}\)
B là biến cố "Trọng đứng đầu hàng", P(B)=\(\dfrac{6!.C\dfrac{1}{2}}{7!}=\dfrac{2}{7}\)
AB là biến cố "Trọng và Cường cùng đứng đầu hàng" P(AB)=\(\dfrac{2!.5!}{7!}=\dfrac{1}{21}\)
A∪B là biến cố "Có ít nhất một trong hai bạn Cường và Trọng đứng ở đầu hàng"
P(A∪B)=P(A)+P(B)−P(A).P(B)=\(\dfrac{11}{21}\)

a)

b) Nhóm chứa giá trị trung vị chiều cao thành viên đội Sao La là \(\begin{array}{*{20}{l}}{\;\left[ {180;185} \right)}\end{array}\).
Nhóm chứa giá trị trung vị chiều cao thành viên đội Kim Ngưu là \(\begin{array}{*{20}{l}}{\;\left[ {185;190} \right)}\end{array}\).

Ta có số liệu thống kê chiều cao thành viên của hai đội như sau:
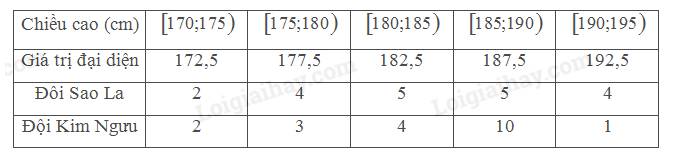
• Chiều cao trung bình của thành viên đội Sao La là:
\(\bar x = \frac{{2.172,5 + 4.177,5 + 5.182,5 + 5.187,5 + 4.192,5}}{{20}} = 183,75\left( {cm} \right)\)
Nhóm chứa số trung vị của đội Sao La là: \(\begin{array}{*{20}{l}}{\;\left[ {180;185} \right)}\end{array}\)
Ta có: \(n = 20;{n_m} = 5;C = 2 + 4 = 6;{u_m} = 180;{u_{m + 1}} = 185\)
Trung vị của chiều cao của thành viên đội Sao La là:
\({M_e} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 180 + \frac{{\frac{{20}}{2} - 6}}{5}.\left( {185 - 180} \right) = 184\left( m \right)\)
• Chiều cao trung bình của thành viên đội Kim Ngưu là:
\(\bar x = \frac{{2.172,5 + 3.177,5 + 4.182,5 + 10.187,5 + 1.192,5}}{{20}} = 183,75\left( {cm} \right)\)
Nhóm chứa số trung vị của đội Kim Ngưu là: \(\begin{array}{*{20}{l}}{\;\left[ {185;190} \right)}\end{array}\)
Ta có: \(n = 20;{n_m} = 10;C = 2 + 3 + 4 = 9;{u_m} = 185;{u_{m + 1}} = 190\)
Trung vị của chiều cao của thành viên đội Kim Ngưu là:
\({M_e} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 185 + \frac{{\frac{{20}}{2} - 9}}{{10}}.\left( {190 - 185} \right) = 185,5\left( m \right)\)
Vậy chiều cao trung bình của hai đội bằng nhau, số trung vị của đội Sao La nhỏ hơn số trung vị của đội Kim Ngưu.


Tham khảo bảng sau:
• Đối với khách hàng nam:
Nhóm chứa mốt của mẫu số liệu trên là nhóm \(\left[ {40;50} \right)\).
Do đó: \({u_m} = 40;{n_{m - 1}} = 6;{n_m} = 10;{n_{m + 1}} = 7;{u_{m + 1}} - {u_m} = 50 - 40 = 10\)
Mốt của mẫu số liệu ghép nhóm là:
\({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right) = 40 + \frac{{10 - 6}}{{\left( {10 - 6} \right) + \left( {10 - 7} \right)}}.10 = 45,7\)
Vậy ta có thể dự đoán khách hàng nam 46 tuổi có nhu cầu mua bảo hiểm nhiều nhất.
• Đối với khách hàng nữ:
Nhóm chứa mốt của mẫu số liệu trên là nhóm \(\left[ {30;40} \right)\).
Do đó: \({u_m} = 30;{n_{m - 1}} = 3;{n_m} = 9;{n_{m + 1}} = 6;{u_{m + 1}} - {u_m} = 40 - 30 = 10\)
Mốt của mẫu số liệu ghép nhóm là:
\({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right) = 30 + \frac{{9 - 3}}{{\left( {9 - 3} \right) + \left( {9 - 6} \right)}}.10 = 36,7\)
Vậy ta có thể dự đoán khách hàng nữ 37 tuổi có nhu cầu mua bảo hiểm nhiều nhất.