Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Để \(4\left(x-8\right)< 0\) thì \(x-8< 0\).
\(\Rightarrow x< 0+8\Rightarrow x< 8\)
\(\Rightarrow x\in\left\{7;6;5;4;3\right\}\)
b) Để \(-3\left(x-2\right)< 0\) thì \(x-2>0\)
\(\Rightarrow x>0+2\Rightarrow x>2\)
\(\Rightarrow x\in\left\{3;4;5;6;7\right\}\)

Viết các tập hợp sau bằng cách liệt kê các phần tử :
a) A = {x∈Nx∈N | 18<x<2118<x<21}
b) B = {x∈N⊛x∈N⊛ | x<4x<4}
c) C = {x∈Nx∈N | 35≤x≤3835≤x≤38}
a, A = { 19;20 }
b, B = { 1;2;3 }
c, C = { 35;36;37;38 }

Bài 3\(x=-2002\):
a.
\(\left|x\right|=2002\)
\(x=\pm2002\)
Vậy \(x=2002\) hoặc \(x=-2002\)
b.
\(\left|x\right|=0\)
\(x=0\)
c.
\(\left|x\right|< 3\)
\(\left|x\right|\in\left\{0;1;2\right\}\)
\(x\in\left\{-2;-2;0;1;2\right\}\)
Chúc bạn học tốt![]()
3. Tìm x biết
a. |x|=2002
=> x = 2002 hoặc -2002
b, |x|=0
=> x = 0
c.|x|<3
=> |x| = {0; 1; 2}
x = {0; 1; -1; 2; -2}
d.|x|>4 và x<-70
=> x < -70
x = {-71; -72, -73; -74; ...}

a)(2;3;4;5;.....;3207
b)tap hop B la tập hợp con của tập hợp A

Bài 1:
\(a.\left|x\right|+\left|6\right|=\left|-27\right|\\ \Leftrightarrow\left|x\right|+6=27\\ \Leftrightarrow\left|x\right|=27-6=21\\ \Leftrightarrow\left\{{}\begin{matrix}x=-21\\x=21\end{matrix}\right.\)
a. |x||x| + |+6||+6| = |−27|
x + 6 = 27
x = 27 - 6
x = 21
Vậy x = 21
b. |−5||−5| . |x||x| = |−20|
5 . x = 20
x = 20 : 5
x 4
Vậy x = 4
c. |x| = |−17| và x > 0
|x| = 17
Vì |x| = 17
nên x = -17 hoặc 17
mà x > 0 => x = 17
Vậy x = 17 hoặc x = -17
d. |x||x| = |23||23| và x < 0
|x| = 23
Vì |x| = 23
nên x = 23 hoặc -23
mà x < 0 => x = -23
e. 12 ≤≤ |x||x| < 15
Vì 12 ≤ |x| < 15
nên x = {12; 13; 14}
Vậy x € {12; 13; 14}
f. |x| > 3
Vì |x| > 3
nên x = -2; -1; 0; 1; 2;
Vậy x € {-2; -1; 1; 2}
a. A=
{
x∈Z|−3<x≤7}
A = {-2; -1; 0; 1; 2; 3; 4; 5; 6; 7}
b. B={x∈Z|3≤|x|<7}
B = {3; 4; 5; 6}
c. C={x∈Z||x|>5}
C = {6; 7; 8; 9; ...}

a) Đúng vì 9 là số tự nhiên
b) Sai vì \( - 6\) là số nguyên âm, không phải là số tự nhiên.
c) Đúng vì \( - 3\) là số nguyên âm nên nó là số nguyên.
d) Đúng vì 0 là số nguyên
e) Đúng vì số 5 là số nguyên dương nên nó là số nguyên.
g) Đúng vì 20 là số tự nhiên.
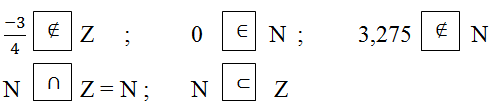
a) \(A = \left\{ {a \in \mathbb{Z}| - 4 < a < - 1} \right\}\)
A là tập hợp các số nguyên a thỏa mãn \( - 4 < a < - 1\).
\( - 4 < a < - 1\) có nghĩa là: a là số nguyên nằm giữa \( - 4\) và \( - 1\). Có các số \( - 3; - 2\).
Vậy \(A = \left\{ { - 3; - 2} \right\}\)
b) \(B = \left\{ {b \in \mathbb{Z}| - 2 < b < 3} \right\}\)
B là tập hợp các số nguyên b thỏa mãn \( - 2 < b < 3\).
\( - 2 < b < 3\) có nghĩa là: b là số nguyên nằm giữa \( - 2\) và \(3\). Có các số \( - 1;0;1;2\).
Vậy \(B = \left\{ { - 1;0;1;2} \right\}\)
c) \(C = \left\{ {c \in \mathbb{Z}| - 3 < c < 0} \right\}\)
C là tập hợp các số nguyên c thỏa mãn \( - 3 < c < 0\).
\( - 3 < c < 0\) có nghĩa là: c là số nguyên nằm giữa \( - 3\) và 0. Có các số \( - 2; - 1\).
Vậy \(C = \left\{ { - 2; - 1} \right\}\)
d) \(D = \left\{ {d \in \mathbb{Z}| - 1 < d < 6} \right\}\)
D là tập hợp các số nguyên d thỏa mãn \( - 1 < d < 6\).
\( - 1 < d < 6\) có nghĩa là: b là số nguyên nằm giữa \( - 1\) và 6. Có các số \(0;1;2;3;4;5\).
Vậy \(D = \left\{ {0;1;2;3;4;5} \right\}\)