Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x là vận tốc của ô tô (x > 0, km/h)
Thời gian ô tô đi từ A đến B là: 50/x (giờ).
Để ô tô đến trước 9h thì ô tô phải đi với thời gian ít hơn: 9 - 7 = 2h hay 50/x < 2
⇔ 50 < 2x (nhân cả hai vế với x > 0)
⇔ 25 < x (chia cả hai vế cho 2).
Vậy để ô tô đến B trước 9 giờ thì ô tô phải chạy với vận tốc x thỏa mãn: x > 25.(km/h)

GỌi x là vận tốc của ô tô (x > 0, tính bằng km/h)
Thời gian đi từ A đến B: 50/x
Để đến B trước 9 giờ thì 50/x < 2
GỌi x là vận tốc của ô tô (x > 0, tính bằng km/h)
Thời gian đi từ A đến B: 50x50x
Để đến B trước 9 giờ thì 50x50x < 2

Giả sử xe đến B vào đúng 12 giờ cùng ngày
\(\Rightarrow t=12-7=5\left(h\right)\) \(\Rightarrow v=\dfrac{s}{t}=\dfrac{50}{5}=10\left(km/h\right)\)
Vậy để ô tô đến trước 12h thì xe phải đi với vận tốc lớn hơn 10km/h

Trl:
Số thời gian ô tô phải đi để đến B là:
11 - 7 = 4 ( giờ)
Vận tốc ô tô phải đi để đến B trước 11giờ là:
108 : 4 = 27(km/giờ)
Đ/s: 27 km/giờ

Gọi độ dài AB là x
Thời gian đi là x/50
Thời gian về là x/60
Theo đề, ta có: x/50-x/60=1/2
=>x=150
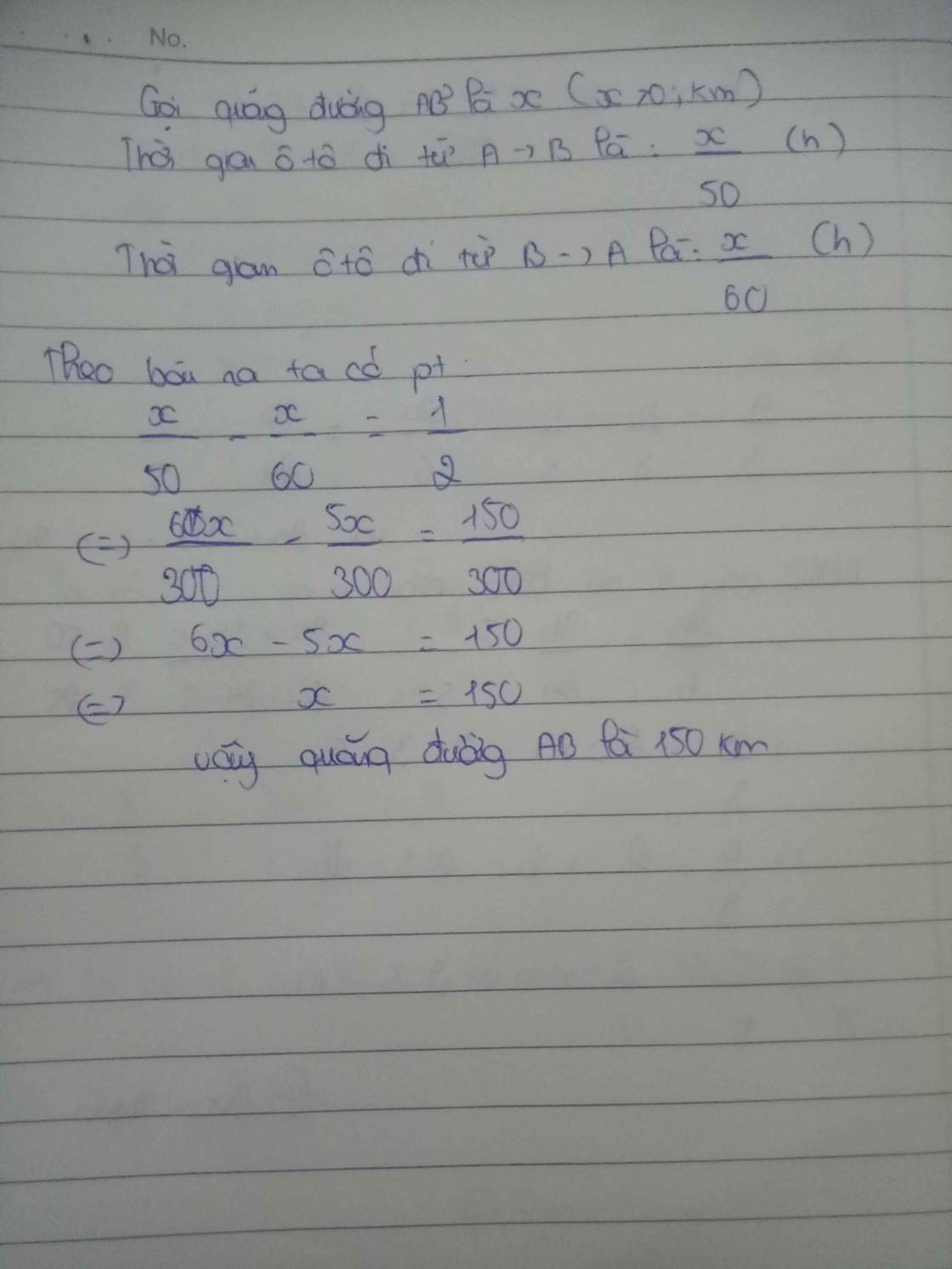
GỌi x là vận tốc của ô tô (x > 0, tính bằng km/h)
Thời gian đi từ A đến B: 50x50x
Để đến B trước 9 giờ thì 50x50x < 2
Gọi x (km/h) là vận tốc của ô tô (x > 0)
Vậy để B đến trước 9 giờ thì ô tô phải chạy với vận tốc x thỏa mãn: x > 25